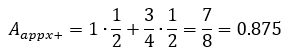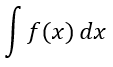martes, 1 de marzo de 2022

Integrales parte 1 (actualizada)

Estimación de áreas

    En pasadas publicaciones tratamos el tema de “áreas y perímetros”. Para figuras geométricas regulares determinar el área es un proceso bastante simple. Existen fórmulas directas que nos permite determinar este valor (el área de un triángulo es igual a la mitad de su base multiplicada por su altura), pero cuando tenemos figuras geométricas irregulares determinar el área es un proceso más complejo.

    Existen figuras irregulares que podemos conocer su área si la dividimos en secciones y sumamos sus partes,


    En la figura de arriba vemos que podemos partir esta imagen en tres regiones y calcular de esta forma su área total.

    Sin embargo, no todas las figuras irregulares las podemos examinar como estas. Existen figuras que no podemos calcular usando esta técnica o simplemente no tenemos la información suficiente.

    En este caso tenemos una función f(x) dada y queremos determinar el área debajo de la curva de la función en el intervalo (a, b). Determinar el área de esta función dependerá del tipo de función que sea f(x), por lo que este problema se puede hacer bastante complicado usando solamente algebra. Por el resto de esta publicación vamos a trabajar una técnica para aproximar el área de funciones como esta. Esta técnica es importante para el desarrollo de la teoría de integración. Vamos a empezar considerando un ejemplo numérico y de esta vamos a extraer las características esenciales para crear nuestra teoría.

    Supongamos que queremos conocer el área de la región sombreada creada por una función y = 1- x2 en el intervalo x = 0 hasta x = 1. En este tipo de casos no existe un método algebraico especifico ni formula que se pueda usar para calcular el área exacta, pero si podemos aproximarla usando un método bastante simple. Podemos tomar nuestra área sombreada y dividirla en regiones usando rectángulos para calcular la aproximación del área. Si decidimos dividir la figura en dos rectángulos entonces tendremos rectángulos con una anchura de 0.5 y su altura dependerá de su ubicación (el valor de x nos permite conocer el valor de y en la ecuación).

    Su área aproximada es la suma de estas dos regiones.

    Esta estimación es mayor que el área real A, ya que los dos rectángulos contienen regiones fuera de la parte sombreada, y esto se suma a la cantidad calculada. decimos que esta es una suma superior porque se obtiene tomando la altura de cada rectángulo como el valor máximo (superior) de la función. Si analizamos la función de izquierda a derecha, tenemos nuestro primer punto donde toca la gráfica y nos movemos hacia la derecha hasta nuestro segundo punto donde toca la gráfica y nos movemos a la derecha otra al siguiente punto y así sucesivamente. De esta manera creamos una suma superior.

    Supongamos que usamos cuatro rectángulos contenidos dentro de la región para estimar el área.

    Esta estimación es más pequeña que el área A ya que todos los rectángulos se encuentran dentro de la región. La suma de estos rectángulos con alturas iguales al valor mínimo de la función se denomina aproximación de suma inferior. En este caso analizamos la figura de derecha a izquierda; el primer punto donde toca la grafica y nos movemos a la izquierda hasta el próximo punto y subimos hasta donde toca la grafica y nos movemos de nuevo a la izquierda hasta el siguiente y subimos donde toca la gráfica y así continuamente.

    No siempre vamos a obtener una suma inferior si nos movemos de derecha a izquierda ni una superior si nos movemos de izquierda a derecha, la es que si calculamos desde el punto mas alto de la gráfica hasta el más pequeño entonces tendremos una suma superior y si contamos desde el punto más pequeño de la grafica hasta el punto mas alto entonces tendremos una suma inferior.

    Al considerar las aproximaciones de suma inferior y superior, no solo obtenemos estimaciones para el área, sino también un límite en el tamaño del posible error en estas estimaciones, ya que el valor real del área se encuentra en algún lugar entre ellos. También obtenemos una mejor aproximación del área al tomar el promedio Aavg de la suma superior y la suma inferior.

    Si analizamos de forma abstracta podemos decir que, en cada una de nuestras sumas calculadas, el intervalo [a, b] sobre el cual se define la función f se subdividió en n subintervalos de igual ancho determinado por ∆x = (b - a)/n y f se evaluó en un punto de cada subintervalo: c1 en el primer subintervalo, c2 en el segundo subintervalo, y así sucesivamente. Entonces todas las sumas finitas del área toman la forma.

    Las opciones para cn podrían maximizar o minimizar el valor de f. Al tomar más y más rectángulos, con cada rectángulo más delgado que antes, parece que estas sumas finitas dan aproximaciones cada vez mejores y cercas al área real. Como el propósito es estar tan cerca del área real como sea posible, el número de rectángulos en el que vamos a dividir nuestra función no será tan simple como tener dos o tres rectángulos, de hecho, estamos hablando de una suma con muchos términos, por lo que escribir todos los términos uno por uno seria una tarea tediosa y hasta imposible si el número de términos es muy grande, pero las matemáticas tienen su propio lenguaje para expresar sumas de cantidades exorbitantemente grandes.

    La notación sigma nos permite escribir una suma con muchos términos en forma compacta.

    La letra griega ∑ (sigma mayúscula correspondiente a la letra S del alfabeto castellano), significa "suma". El índice en el número debajo del símbolo de suma k nos dice dónde comienza la suma y el número de arriba dónde termina.

Ejemplo.

Propiedades y reglas de sumas finitas.

  • Regla de la suma

  • Regla de la resta

  • Regla de multiplicación por una constante

Cualquier valor de c

  • Regla de valor constante 

c es cualquier valor constante


    Por ahora esto ha sido todo. En nuestra próxima publicación continuaremos con el tema usando el mismo ejemplo para calcular su area real. Es bueno tratar este tema despacio ya que es importante que entiendan cada paso si quieren comprender como funcionan las integrales. Si les gusto el tema por favor compartirlo y si tienen sugerencias por favor agregarlo en los comentarios.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

Publicadas por a la/s No hay comentarios.:
Etiquetas: , , , , , , ,

martes, 15 de febrero de 2022

Antiderivada

    Hemos estudiado cómo calcular la derivada de una función, pero qué pasa si queremos saber la función de una derivada dada. En términos propios, diremos que si f es una función, queremos encontrar una función F cuya derivada sea f. si existe la función F, la llamamos la antiderivada de la función f, y este es el vínculo que conecta derivadas e integrales en cálculo.

  • Una función F es una antiderivada de f en un intervalo abierto I si F’(x) = f(x) para todo x en I.

    El proceso de encontrar una antiderivada requiere que pensemos al revés, pero hay derivadas simples que con solo mirarlas podemos identificar su antiderivada.

Ejemplo 1. Funciones y antiderivadas.

f(x) = 2x à F(x) = x2      g(x) = cos(x) à G(x) = sin(x)   h(x) = 1/x à H(x) = ln |x|

    Podemos comprobar las respuestas diferenciando F(x), G(x) y H(x) y ver si obtenemos f(x), g(x) y h(x) de regreso. Sin embargo, estas soluciones no son únicas, existen otras funciones que pueden proporcionar la misma función derivada, como x2 + 1 ó x2 + C para cualquier constante C. uno de los corolarios del Teorema del valor medio nos dice dos (funciones) antiderivadas cualesquiera difieren por una constante. Esto nos permite crear un nuevo teorema para las antiderivadas.

  • Si F es una antiderivada de f en un intervalo I, entonces la antiderivada más general de f en I es 

F(x) + C

(1)

    la antiderivada más general de ƒ sobre I es una familia de funciones cuyas gráficas son traslaciones verticales unas de otras.

Ejemplo 2. Encuentra la antiderivada de f(x) = 3x2.

Como la derivada de x3 es 3x2, la antiderivada general es

F(x) = x3 + C

    El valor de la constante se puede encontrar usando condiciones especiales como las condiciones iniciales. en el ejemplo 2 si queremos que la antiderivada satisfaga F(1) = –1.

F(1) = (1)3 + C = –1

1 + C = –1

C = –2

Por lo tanto la antiderivada de la función 3x2 que satisface F(1) = –1 es.

F(x) = x3– 2

    Al trabajar hacia atrás, podemos derivar fórmulas y reglas para antiderivadas, pero hacer esto requerirá mucho tiempo para examinar múltiples casos y encontrar patrones. Afortunadamente para nosotros, esto ya se ha hecho, así que solo necesitamos memorizar y aprender a trabajar con ellos. Algunas de las reglas más generales para antiderivadas son estas.

Integral Indefinida

    El conjunto de todas las antiderivadas de f se llama integral indefinida y se denota por.

(2)

    El símbolo utilizado aquí es un signo integral, la función f es el integrando y x es la variable de integración. Usando esta notación, podemos reformular la solución del ejemplo 1 de la siguiente manera:

    Esta notación se explorará más en nuestra próxima serie de cálculo y es crucial en el desarrollo de lo que se conoce como el Teorema Fundamental del Cálculo.

Ejemplo 3. Evaluar \int {({x^3} - 4x + 7)\,dx}.

    Podemos calcular cada antiderivada por separado usando la tabla anterior.

Problema de Valor Inicial y Ecuaciones Diferenciales

    Encontrar una antiderivada es lo mismo que encontrar una función que satisfaga la ecuación.

\frac{{dy}}{{dx}} = f(x)

(3)

    A esto se le llama ecuación diferencial. Para resolverlo necesitamos una función y(x) que satisfaga la ecuación. Esta función se encuentra tomando la antiderivada de f(x). la antiderivada más general.

F(x) + C

    Da la solución general de la ecuación diferencial y(x). Si se nos dan condiciones especiales como

y(x0) = y0

    Eso indica el estado inicial de la función, esto quiere decir que la función tiene el valor y0 cuando x = x0. La combinación de una ecuación diferencial y esta condición inicial se denomina problema de valor inicial (PVI), y la solución a este problema son soluciones particulares que satisfacen las condiciones iniciales. En el ejemplo 2, la función y(x) = x3 – 2 es la solución particular de la ecuación diferencial \frac{{dy}}{{dx}} = 3{x^2} satisfaciendo la condición inicial y(1) = –1. Este tipo de problemas se encuentran en todas las ramas de la ciencia.

  • Estudio del crecimiento y decadencia de la población.
  • Absorción de glucosa por el cuerpo.
  • Propagación de epidemias
  • Segunda ley de movimiento de Newton
  • Circuitos RL en electricidad
  • Y mucho más.

    El entendimiento de las antiderivadas se hace más fácil por medio de la practica así que aquí les dejo unos ejercicios para que practiquen y en la próxima publicación les presentare los resultados.

Encuentre las antiderivadas de cada función.

  • x2 - 2x + 1
  • x-4 + 3x2 + 2
  • x-3/2 + x2
  • \sqrt x + \frac{1}{{\sqrt x }}
  • - \frac{1}{2}x - \frac{4}{3}
  • \sin (\pi x) - 3\sin (3x)
  • - \pi \csc \left( {\frac{{\pi x}}{2}} \right) \cdot \cot \left( {\frac{{\pi x}}{2}} \right)

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 




 


Publicadas por a la/s No hay comentarios.:
Etiquetas: , , , ,

martes, 1 de febrero de 2022

Aplicaciones de la derivada 5: Optimización Aplicada

Cuando hablamos de optimización, buscamos respuestas en preguntas como ¿Cuáles son las dimensiones de un rectángulo con perímetro fijo que tiene un área máxima? ¿Cuáles son las dimensiones de la lata cilíndrica menos costosa de un volumen dado? ¿Cuántos artículos se deben producir para lograr la producción más rentable? El problema de la optimización es común en las áreas de economía, física, matemáticas, agricultura, arquitectura e ingeniería civil. En general, podemos reconocer este problema usando palabras clave como máximo, mínimo, mucho, más, etc. En esta sección planeamos ver y analizar casos de optimización desde la perspectiva de las derivadas y cómo se puede aplicar esto a algunos casos.

Los pasos propuestos para resolver un problema verbal y un problema de optimización son muy similares. La idea principal es dividir el problema en secciones que sean fáciles de manipular y puedan llevarnos a las respuestas. Al resolver problemas de optimización, la mejor forma, o la forma más "óptima" de hacerlo, es la siguiente.

  • Leer el problema.
  • Hacer un dibujo del problema.
  • Introducir variables para averiguar qué se sabe y qué buscas.
  • Escribir una ecuación para la cantidad desconocida.
  • Probar puntos críticos y puntos finales en el dominio de la cantidad desconocida.

Probemos esta idea y veamos cómo se puede usar.

Ejemplo 1. Queremos construir una caja usando una lámina de cartón de 14 x 14 pulgadas y cortando pequeños cuadrados congruentes en las esquinas. ¿Qué tamaño debe tener el corte cuadrado desde la esquina para que la caja contenga la mayor cantidad posible?

Paso 1: Lee el problema. La importancia de leer la declaración es encontrar las palabras clave que describen el problema. Lo que sabemos, lo que necesitamos. Al leer este problema, sabemos que queremos construir una caja que sea un objeto tridimensional. Tenemos una hoja bidimensional que se nos da como un cuadrado con una dimensión de 14 x 14 pulgadas, y cortaremos un pequeño cuadrado de las esquinas para que la caja aguante lo más posible. Esta última parte es la que nos dice que se trata de un problema de optimización.

Paso 2: Haz un dibujo del problema. Comenzamos dibujando una hoja bidimensional y etiquetamos los lados respectivos de cómo queremos romperla. y tendremos la siguiente imagen.

Paso 3: introduce variables para averiguar qué se sabe y qué estás buscando. Como no sabemos qué tan grandes queremos que sean las esquinas cortadas (que es lo que necesitamos resolver), lo llamamos x (ya que los términos desconocidos deben escribirse como una variable), y la imagen cambiará así.

Entonces, si cortamos las esquinas cuadradas y doblamos la hoja para crear la caja, nuestros lados tendrán una longitud de 14 – 2x ya que sacamos una pieza de cada esquina con una longitud de x; y nuestra altura será x. Ahora nuestra caja tridimensional tiene las siguientes unidades.

Paso 4: Escribe una ecuación para la cantidad desconocida. Para encontrar qué tan grande debe ser la esquina cortada cuadrada, tenemos que calcular el volumen de la caja, debemos escribirlo en términos de la longitud x.

V(x) = ancho x largo x alto

V(x) = x (14 – 2x)2

V(x) = 4x (7 – x)2 = 4x (49 – 14x + x2) = 196x – 56x2 + 4x3

Por inspección podemos ver que x ≤ 7 ya que los lados de la hoja miden 14 in de largo. Podemos deducir que el dominio de x está en el intervalo 0 ≤ x ≤ 7.

Paso 5: pruebe los puntos críticos y los puntos finales en el dominio de la cantidad desconocida. Examinamos la primera derivada de V con respecto a x y encontramos dónde la derivada es cero.


Factorizando

Lo que nos da los puntos x = 7 y x = 7/3. Cuando evaluamos el punto final x = 7 obtenemos un valor de cero que concuerda con el teorema del valor medio, mientras evaluamos el punto crítico x = 7/3 obtenemos 203.3 por lo tanto el volumen máximo es 203.3 in2 y el corte debe ser 7/3 en un lado.

 

Ejemplo 2. Se va a inscribir un rectángulo en un semicírculo de radio 3. ¿Cuál es el área más grande que puede tener el rectángulo y cuáles son sus dimensiones?

Paso 1. El problema es preguntarnos qué tan grande puede ser un rectángulo para caber dentro de un semicírculo de radio 3.

Paso 2.

Paso 3. Como no conocemos las dimensiones del rectángulo, podemos nombrar su longitud como x para el lado horizontal, mientras que el lado vertical se puede encontrar usando el teorema de Pitágoras. 

Paso 4. Ahora podemos escribir expresiones para la altura, la longitud y el área del rectángulo.

Longitud: 2x,           Altura: √(9 - x2),            Área: 2x√(9 - x2)

Dado que el semicírculo establece un límite para la longitud, el dominio debe estar en el intervalo 0 ≤ x ≤ 3.

Paso 5. Para encontrar el valor máximo absoluto de la función debemos evaluar la derivada de la función del área cuando es cero.

No está definido cuando x = 3 pero aún podemos encontrar los ceros.

Multiplicando ambos lados por   \sqrt {9 - {x^2}}  tenemos

Solo de los valores posibles cuentan. El positivo está en el dominio establecido, por lo que este es un punto crítico. Ahora podemos evaluar el área en este punto crítico así como la longitud y la altura.

Aunque parece una expresión algebraica intimidante, su respuesta y solución son muy simples. La solución final nos dice que el área tiene un valor máximo de 9 cuando la longitud del rectángulo es 3√2 y su altura es 3√(1/2).

 

Ejemplo 3. Queremos diseñar una lata de medio litro con forma de cilindro circular recto. ¿Qué dimensiones utilizarán la menor cantidad de material? Exprese su respuesta en centímetros.

Para encontrar las dimensiones de una lata cilíndrica, debemos convertir los litros en una forma de volumen con centímetros. Por suerte la relación es estándar.

1 litro = 1000 cm3 à ½ litro = 500 cm3

El volumen de la lata (cilindro) está dado por

Donde r es el radio y h es la altura de la lata. El área de superficie del cilindro se calcula usando.

Ahora la parte más importante es el significado de la frase "menos material". Para una primera aproximación podemos ignorar el espesor del material y el desperdicio en la fabricación pero aun así tenemos el problema de tratar con dos variables. Podemos resolver una de las ecuaciones para una variable y sustituirla en la siguiente ecuación de esa manera solo tenemos una variable de la que preocuparnos. Entonces, resolvamos la ecuación de volumen para la Altura.

Por lo tanto,

Ahora podemos encontrar un valor de r > 0 que maximice el valor de A, y esto nos permitirá encontrar las mejores medidas para nuestra lata. Dado que A es derivable sin extremos, puede tener un valor mínimo donde su primera derivada es cero.

Observe en el gráfico que para r pequeño (un recipiente cilíndrico alto y delgado), el término 1000/r domina y A es grande. Para r grande (un recipiente cilíndrico corto y ancho), el término 2πr2 domina y A nuevamente es grande.

¿Qué sucede en  r = \sqrt[3]{{500/\pi }}? Examinemos la segunda derivada.

Es cóncava hacia arriba en todo el dominio de A, por lo que este valor es de hecho un mínimo absoluto. Podemos usar esto para encontrar el valor de la altura de la lata.

con un poco de manipulación del álgebra, obtenemos

la lata de medio litro que usa menos material tiene una altura igual a su radio con r ≈ 4.3 cm y h ≈ 4.3 cm.

La optimización es muy práctica para situaciones de la vida real y entenderla les será de gran utilidad. En la próxima publicación estaré introduciendo la idea de antiderivadas. Esta será fundamental para entender las integrales que son nuestro próximo tema. Si les gusto el contenido por favor compartirlo con otras personas y si tienen sugerencia las puedes escribir en la sección de comentarios. De verdad queremos escuchar su opinión. Será de gran ayuda.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

Publicadas por a la/s No hay comentarios.:
Etiquetas: , , , , , , , ,
Suscribirse a: Entradas (Atom)