Aplicaciones de la derivada 5: Optimización Aplicada

Cuando hablamos de optimización, buscamos respuestas en preguntas como ¿Cuáles son las dimensiones de un rectángulo con perímetro fijo que tiene un área máxima? ¿Cuáles son las dimensiones de la lata cilíndrica menos costosa de un volumen dado? ¿Cuántos artículos se deben producir para lograr la producción más rentable? El problema de la optimización es común en las áreas de economía, física, matemáticas, agricultura, arquitectura e ingeniería civil. En general, podemos reconocer este problema usando palabras clave como máximo, mínimo, mucho, más, etc. En esta sección planeamos ver y analizar casos de optimización desde la perspectiva de las derivadas y cómo se puede aplicar esto a algunos casos.

Los pasos propuestos para resolver un problema verbal y un problema de optimización son muy similares. La idea principal es dividir el problema en secciones que sean fáciles de manipular y puedan llevarnos a las respuestas. Al resolver problemas de optimización, la mejor forma, o la forma más "óptima" de hacerlo, es la siguiente.

• Leer el problema.
• Hacer un dibujo del problema.
• Introducir variables para averiguar qué se sabe y qué buscas.
• Escribir una ecuación para la cantidad desconocida.
• Probar puntos críticos y puntos finales en el dominio de la cantidad desconocida.

Probemos esta idea y veamos cómo se puede usar.

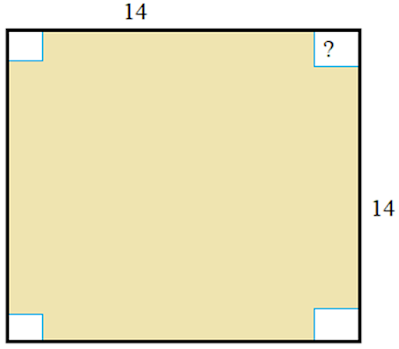
Ejemplo 1. Queremos construir una caja usando una lámina de cartón de 14 x 14 pulgadas y cortando pequeños cuadrados congruentes en las esquinas. ¿Qué tamaño debe tener el corte cuadrado desde la esquina para que la caja contenga la mayor cantidad posible?

Paso 1: Lee el problema. La importancia de leer la declaración es encontrar las palabras clave que describen el problema. Lo que sabemos, lo que necesitamos. Al leer este problema, sabemos que queremos construir una caja que sea un objeto tridimensional. Tenemos una hoja bidimensional que se nos da como un cuadrado con una dimensión de 14 x 14 pulgadas, y cortaremos un pequeño cuadrado de las esquinas para que la caja aguante lo más posible. Esta última parte es la que nos dice que se trata de un problema de optimización.

Paso 2: Haz un dibujo del problema. Comenzamos dibujando una hoja bidimensional y etiquetamos los lados respectivos de cómo queremos romperla. y tendremos la siguiente imagen.

Paso 3: introduce variables para averiguar qué se sabe y qué estás buscando. Como no sabemos qué tan grandes queremos que sean las esquinas cortadas (que es lo que necesitamos resolver), lo llamamos x (ya que los términos desconocidos deben escribirse como una variable), y la imagen cambiará así.

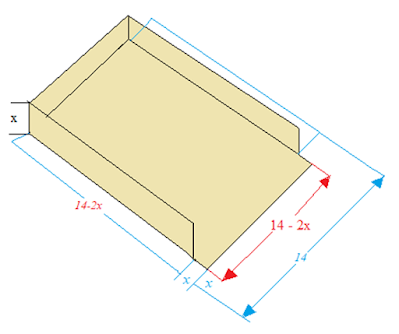
Entonces, si cortamos las esquinas cuadradas y doblamos la hoja para crear la caja, nuestros lados tendrán una longitud de 14 – 2x ya que sacamos una pieza de cada esquina con una longitud de x; y nuestra altura será x. Ahora nuestra caja tridimensional tiene las siguientes unidades.

Paso 4: Escribe una ecuación para la cantidad desconocida. Para encontrar qué tan grande debe ser la esquina cortada cuadrada, tenemos que calcular el volumen de la caja, debemos escribirlo en términos de la longitud x.

V(x) = ancho x largo x alto

V(x) = x (14 – 2x)²

V(x) = 4x (7 – x)² = 4x (49 – 14x + x²) = 196x – 56x² + 4x³

Por inspección podemos ver que x ≤ 7 ya que los lados de la hoja miden 14 in de largo. Podemos deducir que el dominio de x está en el intervalo 0 ≤ x ≤ 7.

Paso 5: pruebe los puntos críticos y los puntos finales en el dominio de la cantidad desconocida. Examinamos la primera derivada de V con respecto a x y encontramos dónde la derivada es cero.

Factorizando

Lo que nos da los puntos x = 7 y x = 7/3. Cuando evaluamos el punto final x = 7 obtenemos un valor de cero que concuerda con el teorema del valor medio, mientras evaluamos el punto crítico x = 7/3 obtenemos 203.3 por lo tanto el volumen máximo es 203.3 in² y el corte debe ser 7/3 en un lado.

 

Ejemplo 2. Se va a inscribir un rectángulo en un semicírculo de radio 3. ¿Cuál es el área más grande que puede tener el rectángulo y cuáles son sus dimensiones?

Paso 1. El problema es preguntarnos qué tan grande puede ser un rectángulo para caber dentro de un semicírculo de radio 3.

Paso 2.

Paso 3. Como no conocemos las dimensiones del rectángulo, podemos nombrar su longitud como x para el lado horizontal, mientras que el lado vertical se puede encontrar usando el teorema de Pitágoras. 

Paso 4. Ahora podemos escribir expresiones para la altura, la longitud y el área del rectángulo.

Longitud: 2x,           Altura: √(9 - x²),            Área: 2x√(9 - x²)

Dado que el semicírculo establece un límite para la longitud, el dominio debe estar en el intervalo 0 ≤ x ≤ 3.

Paso 5. Para encontrar el valor máximo absoluto de la función debemos evaluar la derivada de la función del área cuando es cero.

No está definido cuando x = 3 pero aún podemos encontrar los ceros.

Multiplicando ambos lados por     tenemos

Solo de los valores posibles cuentan. El positivo está en el dominio establecido, por lo que este es un punto crítico. Ahora podemos evaluar el área en este punto crítico así como la longitud y la altura.

Aunque parece una expresión algebraica intimidante, su respuesta y solución son muy simples. La solución final nos dice que el área tiene un valor máximo de 9 cuando la longitud del rectángulo es 3√2 y su altura es 3√(1/2).

 

Ejemplo 3. Queremos diseñar una lata de medio litro con forma de cilindro circular recto. ¿Qué dimensiones utilizarán la menor cantidad de material? Exprese su respuesta en centímetros.

Para encontrar las dimensiones de una lata cilíndrica, debemos convertir los litros en una forma de volumen con centímetros. Por suerte la relación es estándar.

1 litro = 1000 cm³ à ½ litro = 500 cm³

El volumen de la lata (cilindro) está dado por

Donde r es el radio y h es la altura de la lata. El área de superficie del cilindro se calcula usando.

Ahora la parte más importante es el significado de la frase "menos material". Para una primera aproximación podemos ignorar el espesor del material y el desperdicio en la fabricación pero aun así tenemos el problema de tratar con dos variables. Podemos resolver una de las ecuaciones para una variable y sustituirla en la siguiente ecuación de esa manera solo tenemos una variable de la que preocuparnos. Entonces, resolvamos la ecuación de volumen para la Altura.

Por lo tanto,

Ahora podemos encontrar un valor de r > 0 que maximice el valor de A, y esto nos permitirá encontrar las mejores medidas para nuestra lata. Dado que A es derivable sin extremos, puede tener un valor mínimo donde su primera derivada es cero.

Observe en el gráfico que para r pequeño (un recipiente cilíndrico alto y delgado), el término 1000/r domina y A es grande. Para r grande (un recipiente cilíndrico corto y ancho), el término 2πr² domina y A nuevamente es grande.

¿Qué sucede en  ? Examinemos la segunda derivada.

Es cóncava hacia arriba en todo el dominio de A, por lo que este valor es de hecho un mínimo absoluto. Podemos usar esto para encontrar el valor de la altura de la lata.

con un poco de manipulación del álgebra, obtenemos

la lata de medio litro que usa menos material tiene una altura igual a su radio con r ≈ 4.3 cm y h ≈ 4.3 cm.

La optimización es muy práctica para situaciones de la vida real y entenderla les será de gran utilidad. En la próxima publicación estaré introduciendo la idea de antiderivadas. Esta será fundamental para entender las integrales que son nuestro próximo tema. Si les gusto el contenido por favor compartirlo con otras personas y si tienen sugerencia las puedes escribir en la sección de comentarios. De verdad queremos escuchar su opinión. Será de gran ayuda.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

• Facebook: https://www.facebook.com/AprendeMatematicasJMD
• Twitter: @JMDciencias
• Correo: institutodecienciasjmd@hotmail.com

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

• Facebook: https://www.facebook.com/JMDFisica
• Blogger: jmdfisica.blogspot.com

Aplicaciones de la Derivada 4: Concavidad y Bosquejo de Curvas

    Hemos visto cómo la primera derivada nos dice dónde está aumentando y dónde está disminuyendo una función y si un máximo o un mínimo local ocurre en un punto crítico. En esta sección veremos que la segunda derivada nos da información sobre cómo se dobla o gira la gráfica de una función diferenciable.

    Con este conocimiento sobre la primera y segunda derivadas, podremos dibujar una gráfica precisa de una función. Al organizar todas estas ideas en un procedimiento coherente, damos un método para dibujar gráficos.

    Analicemos la gráfica de la función y = x³.

    Como podemos apreciar, la curva asciende a medida que aumenta x, pero las porciones definidas en los intervalos (-∞, 0) y (0, ∞) giran de diferente manera. De izquierda a nuestro origen la curva gira a nuestra derecha y cae debajo de su tangente, desde el origen hacia la derecha, la curva gira a la izquierda y se eleva por encima de su tangente. La pendiente de la tangente disminuye en el intervalo (-∞, 0) y aumenta en el intervalo (0, ∞). Esta flexión de la curva es lo que llamamos concavidad.

    La gráfica de una función diferenciable y = f (x) es

• Cóncavo hacia arriba si f 'aumenta en el intervalo dado.
• Cóncavo hacia abajo si f 'está disminuyendo en el intervalo dado.

Si la función tiene una segunda derivada, podemos aplicar nuestro tercer corolario para obtener:

• Si  f “ >  0 en el intervalo dado, la gráfica de f es cóncava hacia arriba.
• Si  f “ < 0 en el intervalo dado, la gráfica de f es cóncava hacia abajo.

    Nuestra gráfica de y = x³ es cóncava hacia abajo en (-∞, 0) donde y '' = 6x < 0 y cóncava hacia arriba en (0, ∞) donde y '' = 6x > 0. El punto donde la concavidad cambia en el gráfico y tiene una tangente se llama un punto de inflexión. En nuestro ejemplo, nuestro gráfico cambia de concavidad en x = 0 pero no tiene una línea tangente en él, por lo que este no es un punto de inflexión.

    Ejemplo: Determine la concavidad de y = 3 + sen x en [0, 2π] y encuentre su punto de inflexión.

    Calculando la segunda derivada tenemos y '' = - sin x. Tenemos ceros en 0, π y 2π, por lo que podemos construir intervalos (0, π) y (π, 2π). Y tenemos esa y '' = - sin x es negativo en el intervalo (0, π) por lo que es cóncavo hacia abajo y positivo en los intervalos (π, 2π) por lo que es cóncavo hacia arriba.

    La curva cambia de concavidad en el punto (π, 3) y en este punto tiene una recta tangente de pendiente -1, que es su punto de inflexión.

    Observamos que la segunda derivada es cero en el punto de inflexión. Generalmente, si la segunda derivada existe en un punto de inflexión (c, f (c)), entonces f '' (c) = 0 o f '' (c) Con esto ahora podemos crear una prueba de la segunda derivada para el teorema de los extremos locales.

    Suponga que f’’ es continuo en un intervalo abierto que contiene x = c.

1. Si f’(c) = 0 y f’ (c) < 0, entonces f tiene un máximo local en x = c.

2. Si f’(c) = 0 y f’ (c) > 0, entonces f tiene un mínimo local en x = c.

3. Si  f’(c) = 0 y f’ (c) < 0, entonces la prueba falla. La función f puede tener un máximo local, un mínimo local o ninguno.

Ejemplo. Dibuja una gráfica de la función f (x) = x⁴ - 4x³ + 10.

    Lo primero que analizamos es el dominio de la función y encontramos que esta función es continua en todas partes, por lo tanto su dominio es (-∞, ∞), por lo que los puntos críticos ocurren solo en los cero de la derivada.

f’(x) = 4x³ - 12x² = 4x²(x - 3)

    Encontramos que la primera derivada es cero en x = 0 y x = 3. Ahora con los puntos críticos creamos subdivisiones para encontrar las regiones donde está aumentando o disminuyendo.

- ∞ < x < 0 es negativo, por lo que es decreciente

0 < x < 3 es negativo, por lo que es decreciente

x > 3 es positivo, por lo que aumenta

    Sí aplicamos la prueba de la primera derivada, encontramos un mínimo local en x = 3 pero no un extremo en x = 0

    tomamos ahora la segunda derivada y obtenemos f’’ (x) = 12x² - 24x = 12x (x - 2) con ceros en x = 0 y x = 2. Si analizamos las regiones creadas por estos puntos, podemos encontrar dónde la función es cóncava hacia arriba o cóncava hacia abajo.

-∞ < x < 0 es positivo, por lo que es cóncavo hacia arriba

0 < x < 2 es negativo, por lo que es cóncavo hacia abajo

x > 2 es positivo, por lo que es cóncavo hacia arriba.

    Para resumir la información que adquirimos, creamos las siguientes tablas junto con la forma general del gráfico

x < 0	0 < x < 2	2 < x < 3	x > 3
Decreciente Cóncava arriba	Decreciente Cóncavo hacia abajo	Decreciente Cóncava arriba	Creciente Cóncava arriba

Descripcion general de la grafica del problema.

    Como vemos una gráfica puede tener cualquiera de las siguientes combinaciones.

Procedimiento para graficar y = f (x)

1. Identifique el dominio de f y las simetrías que pueda tener la curva.

2. Encuentra las derivadas y’ y y’’.

3. Encuentre los puntos críticos de f, si los hay, e identifique el comportamiento de la función en cada uno.

4. Encuentre dónde la curva aumenta y disminuye.

5. Encuentre los puntos de inflexión, si ocurre alguno, y determine la concavidad de la curva.

6. Identifique cualquier asíntota que pueda existir.

    la noción de concavidad es importante en la teoría y la economía de la optimización. Otra aplicación de la concavidad es en física para determinar la aceleración dada una gráfica de posición versus tiempo. Dado que la aceleración es la segunda derivada de la posición.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

• Facebook: https://www.facebook.com/AprendeMatematicasJMD
• Twitter: @JMDciencias
• Correo: institutodecienciasjmd@hotmail.com

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

• Facebook: https://www.facebook.com/JMDFisica
• Blogger: jmdfisica.blogspot.com