Aplicaciones de la derivada 5: Optimización Aplicada

Cuando hablamos de optimización, buscamos respuestas en preguntas como ¿Cuáles son las dimensiones de un rectángulo con perímetro fijo que tiene un área máxima? ¿Cuáles son las dimensiones de la lata cilíndrica menos costosa de un volumen dado? ¿Cuántos artículos se deben producir para lograr la producción más rentable? El problema de la optimización es común en las áreas de economía, física, matemáticas, agricultura, arquitectura e ingeniería civil. En general, podemos reconocer este problema usando palabras clave como máximo, mínimo, mucho, más, etc. En esta sección planeamos ver y analizar casos de optimización desde la perspectiva de las derivadas y cómo se puede aplicar esto a algunos casos.

Los pasos propuestos para resolver un problema verbal y un problema de optimización son muy similares. La idea principal es dividir el problema en secciones que sean fáciles de manipular y puedan llevarnos a las respuestas. Al resolver problemas de optimización, la mejor forma, o la forma más "óptima" de hacerlo, es la siguiente.

• Leer el problema.
• Hacer un dibujo del problema.
• Introducir variables para averiguar qué se sabe y qué buscas.
• Escribir una ecuación para la cantidad desconocida.
• Probar puntos críticos y puntos finales en el dominio de la cantidad desconocida.

Probemos esta idea y veamos cómo se puede usar.

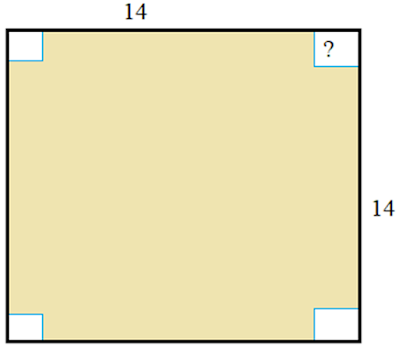
Ejemplo 1. Queremos construir una caja usando una lámina de cartón de 14 x 14 pulgadas y cortando pequeños cuadrados congruentes en las esquinas. ¿Qué tamaño debe tener el corte cuadrado desde la esquina para que la caja contenga la mayor cantidad posible?

Paso 1: Lee el problema. La importancia de leer la declaración es encontrar las palabras clave que describen el problema. Lo que sabemos, lo que necesitamos. Al leer este problema, sabemos que queremos construir una caja que sea un objeto tridimensional. Tenemos una hoja bidimensional que se nos da como un cuadrado con una dimensión de 14 x 14 pulgadas, y cortaremos un pequeño cuadrado de las esquinas para que la caja aguante lo más posible. Esta última parte es la que nos dice que se trata de un problema de optimización.

Paso 2: Haz un dibujo del problema. Comenzamos dibujando una hoja bidimensional y etiquetamos los lados respectivos de cómo queremos romperla. y tendremos la siguiente imagen.

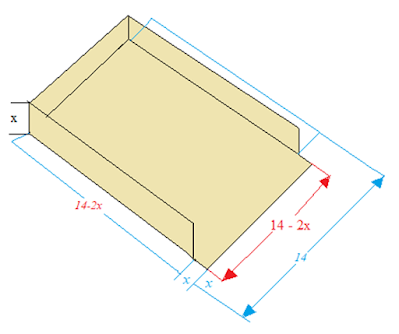
Paso 3: introduce variables para averiguar qué se sabe y qué estás buscando. Como no sabemos qué tan grandes queremos que sean las esquinas cortadas (que es lo que necesitamos resolver), lo llamamos x (ya que los términos desconocidos deben escribirse como una variable), y la imagen cambiará así.

Entonces, si cortamos las esquinas cuadradas y doblamos la hoja para crear la caja, nuestros lados tendrán una longitud de 14 – 2x ya que sacamos una pieza de cada esquina con una longitud de x; y nuestra altura será x. Ahora nuestra caja tridimensional tiene las siguientes unidades.

Paso 4: Escribe una ecuación para la cantidad desconocida. Para encontrar qué tan grande debe ser la esquina cortada cuadrada, tenemos que calcular el volumen de la caja, debemos escribirlo en términos de la longitud x.

V(x) = ancho x largo x alto

V(x) = x (14 – 2x)²

V(x) = 4x (7 – x)² = 4x (49 – 14x + x²) = 196x – 56x² + 4x³

Por inspección podemos ver que x ≤ 7 ya que los lados de la hoja miden 14 in de largo. Podemos deducir que el dominio de x está en el intervalo 0 ≤ x ≤ 7.

Paso 5: pruebe los puntos críticos y los puntos finales en el dominio de la cantidad desconocida. Examinamos la primera derivada de V con respecto a x y encontramos dónde la derivada es cero.

Factorizando

Lo que nos da los puntos x = 7 y x = 7/3. Cuando evaluamos el punto final x = 7 obtenemos un valor de cero que concuerda con el teorema del valor medio, mientras evaluamos el punto crítico x = 7/3 obtenemos 203.3 por lo tanto el volumen máximo es 203.3 in² y el corte debe ser 7/3 en un lado.

 

Ejemplo 2. Se va a inscribir un rectángulo en un semicírculo de radio 3. ¿Cuál es el área más grande que puede tener el rectángulo y cuáles son sus dimensiones?

Paso 1. El problema es preguntarnos qué tan grande puede ser un rectángulo para caber dentro de un semicírculo de radio 3.

Paso 2.

Paso 3. Como no conocemos las dimensiones del rectángulo, podemos nombrar su longitud como x para el lado horizontal, mientras que el lado vertical se puede encontrar usando el teorema de Pitágoras. 

Paso 4. Ahora podemos escribir expresiones para la altura, la longitud y el área del rectángulo.

Longitud: 2x,           Altura: √(9 - x²),            Área: 2x√(9 - x²)

Dado que el semicírculo establece un límite para la longitud, el dominio debe estar en el intervalo 0 ≤ x ≤ 3.

Paso 5. Para encontrar el valor máximo absoluto de la función debemos evaluar la derivada de la función del área cuando es cero.

No está definido cuando x = 3 pero aún podemos encontrar los ceros.

Multiplicando ambos lados por     tenemos

Solo de los valores posibles cuentan. El positivo está en el dominio establecido, por lo que este es un punto crítico. Ahora podemos evaluar el área en este punto crítico así como la longitud y la altura.

Aunque parece una expresión algebraica intimidante, su respuesta y solución son muy simples. La solución final nos dice que el área tiene un valor máximo de 9 cuando la longitud del rectángulo es 3√2 y su altura es 3√(1/2).

 

Ejemplo 3. Queremos diseñar una lata de medio litro con forma de cilindro circular recto. ¿Qué dimensiones utilizarán la menor cantidad de material? Exprese su respuesta en centímetros.

Para encontrar las dimensiones de una lata cilíndrica, debemos convertir los litros en una forma de volumen con centímetros. Por suerte la relación es estándar.

1 litro = 1000 cm³ à ½ litro = 500 cm³

El volumen de la lata (cilindro) está dado por

Donde r es el radio y h es la altura de la lata. El área de superficie del cilindro se calcula usando.

Ahora la parte más importante es el significado de la frase "menos material". Para una primera aproximación podemos ignorar el espesor del material y el desperdicio en la fabricación pero aun así tenemos el problema de tratar con dos variables. Podemos resolver una de las ecuaciones para una variable y sustituirla en la siguiente ecuación de esa manera solo tenemos una variable de la que preocuparnos. Entonces, resolvamos la ecuación de volumen para la Altura.

Por lo tanto,

Ahora podemos encontrar un valor de r > 0 que maximice el valor de A, y esto nos permitirá encontrar las mejores medidas para nuestra lata. Dado que A es derivable sin extremos, puede tener un valor mínimo donde su primera derivada es cero.

Observe en el gráfico que para r pequeño (un recipiente cilíndrico alto y delgado), el término 1000/r domina y A es grande. Para r grande (un recipiente cilíndrico corto y ancho), el término 2πr² domina y A nuevamente es grande.

¿Qué sucede en  ? Examinemos la segunda derivada.

Es cóncava hacia arriba en todo el dominio de A, por lo que este valor es de hecho un mínimo absoluto. Podemos usar esto para encontrar el valor de la altura de la lata.

con un poco de manipulación del álgebra, obtenemos

la lata de medio litro que usa menos material tiene una altura igual a su radio con r ≈ 4.3 cm y h ≈ 4.3 cm.

La optimización es muy práctica para situaciones de la vida real y entenderla les será de gran utilidad. En la próxima publicación estaré introduciendo la idea de antiderivadas. Esta será fundamental para entender las integrales que son nuestro próximo tema. Si les gusto el contenido por favor compartirlo con otras personas y si tienen sugerencia las puedes escribir en la sección de comentarios. De verdad queremos escuchar su opinión. Será de gran ayuda.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

• Facebook: https://www.facebook.com/AprendeMatematicasJMD
• Twitter: @JMDciencias
• Correo: institutodecienciasjmd@hotmail.com

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

• Facebook: https://www.facebook.com/JMDFisica
• Blogger: jmdfisica.blogspot.com

Aplicaciones de la Derivada 3: Funciones monótonas y la Prueba de la Primera Derivada

    A la hora de hacer la gráfica de una función en algebra nos han enseñado a usar diferentes valores de x para encontrar suficientes valores de y que nos permitan crear una gráfica a partir de la unión de los puntos o simplemente memorizar la forma de la gráfica, sin embargo existe un método más simple y consistente para crear graficas e incluso aprender información adicional sobre la gráfica.

    Uno de los aspectos importantes a conocer en una grafica es ver donde la grafica cambia (aumenta o disminuye). Con excepción de la grafica de la pendiente, las graficas por lo general tienen este patrón de incremento (de izquierda a derecha) o disminución (de izquierda a derecha) en un intervalo. Este tipo de funciones son llamadas funciones monótonas y existe un tercer corolario del teorema del valor medio que nos permite identificar estas propiedades.

• Supongamos que f es continua en [a, b] y diferenciable en (a, b). Si f’(x) > 0 en cada punto x en (a, b), entonces f esta aumentado en [a, b]; si f’(x) < 0 en cada punto x (a, b), entonces f está disminuyendo.

    Para recordarles, cuando usamos la expresión f’(x) nos referimos a la derivada de la función .

    Para comprobar esto elegimos dos puntos x₁ y x₂ en [a, b] con x₁ y x₂ y aplicando el teorema del valor medio tenemos que

Se puede reescribir como

    Para un arbitrario valor c entre x₁ y x₂. El signo del lado derecho es determinado por f’(c) ya que x₂ – x₁ es positivo pues x₁ < x₂ y por lo tanto f(x₂) > f(x₁) si f’ es positivo y f(x₂) < f(x₁) si f’ es negativo.

    Ejemplo. Encuentre los puntos críticos de f(x) = x³ – 12x – 5 e identifica donde f esta aumentando y disminuyendo.

    Para encontrar los puntos críticos debemos evaluar la derivada cuando es cero.

f(x) = x³ – 12x – 5

f’(x) = 3x² – 12 = 3(x² – 4)

f’(x) = 0 = 3(x² – 4)

3(x – 2) (x + 2) = 0

    Es cero cuando x = –2 y x = 2. Estos puntos críticos subdividen el dominio en los intervalos (–∞, –2), (–2, 2), (2, ∞). Para determinar si aumenta o disminuye debemos evaluar las regiones eligiendo un punto en ella y determinando su signo.

• –∞ < x < –2 elegimos x = –3 (esto es arbitrario)

f’ (–3) = 3(–3 + 2) (–3 – 2) = +15

como el signo es positivo esto indica que está aumentando.

• –2 < x < 2 elegimos x = 0

f’ (0) = 3(0 + 2) (0 – 2) = –12

como el signo es negativo esto indica que está disminuyendo.

• 2 < x < ∞ elegimos x = 3

f’ (3) = 3(3 + 2) (3 – 2) = +15

como el signo es positivo esto indica que está aumentando.

    De forma grafica podemos representarlo de la siguiente forma.

    Una función aumenta o disminuye sobre una región no en un punto.

Prueba de la primera derivada para extremos locales

    Si analizamos la grafica presentada arriba veremos algunas características interesantes con respecto a los valores mínimos y máximos. Estas observaciones las podemos agrupar y crear la prueba de la primera derivada para los extremos locales.

    Supongamos que c es un punto crítico de una función continua y que es diferenciable en cada punto de un intervalo que contiene c.

1.      Si f’ cambia de negativo a positivo en c entonces f tiene un mínimo local.

2.      Si f’ cambia de positivo a negativo en c entonces f tiene máximo local.

3.      Si f’ no cambia en c entonces f no tiene extremos locales en c.

    En la gráfica podemos ver que c₃ contiene un mínimo local mientras c₂ es un máximo local y los puntos c₁ y c₅ no contienen extremos locales.

    Ejemplo. Encuentra los puntos críticos de f(x) = (x² – 3) e^x. Identifica los intervalos donde esa aumentando y disminuyendo. Encuentra valores extremos y absolutos si los hay.

Primero debemos buscar su derivada.

Podemos usar la regla del producto para ello.

= 2xe^x + (x² – 3) e^x

f' (x) = (x² + 2x –3) e^x

Como e^x nunca es cero, la derivada será cero sí.  

x² + 2x – 3

factorizando

(x + 3) (x – 1) = 0

    Los puntos críticos están en x = –3 y x = 1 así que nuestro dominio se subdivide en las regiones –∞ < x < –3, –3 < x < 1 y 1 < x < ∞.

• –∞ < x < –3 elegimos x = –4 (una vez más, esto es arbitrario)

f’ (–4) = ((–4)²+2(–4) –3) e^–4 = +5e^–4

como el signo es positivo esto indica que está aumentando.

• –3 < x < 1 elegimos x = 0

f’ (0) = ((0)²+2(0) – 3) e⁰ = –3

como el signo es negativo esto indica que está disminuyendo.

• 1 < x < ∞ elegimos x = 2

f’ (2) = ((2)² + 2(2) – 3) e² = +5e²

como el signo es positivo esto indica que está aumentando.

    Si evaluamos los valores de los puntos críticos tenemos que x = 1 f (1) = –2e es el valor más pequeño que obtenemos pero x = –3 f (–3) = 6e^–3 no es el valor mas alto por lo que conocemos que tenemos un mínimo absoluto pero no un máximo absoluto.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

• Facebook: https://www.facebook.com/AprendeMatematicasJMD
• Twitter: @JMDciencias
• Correo: institutodecienciasjmd@hotmail.com

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

• Facebook: https://www.facebook.com/JMDFisica
• Blogger: jmdfisica.blogspot.com

Aplicaciones de la Derivada 2: Teorema del Valor Medio

    ¿Pueden existir funciones complicadas cuyas derivadas siempre sean igual a cero? Si dos funciones tienen la misma derivada sobre un intervalo determinado ¿Cómo estas están relacionadas? Antes de que llegue al final de esta publicación sabrá la respuesta a estas dos preguntas. Empezaremos analizando algo conocido el teorema de Rolle. Este postula lo siguiente:

• Supongamos que y = f(x) es continua en cada punto del intervalo cerrado [a, b] y diferenciable en cada punto de su interior (a, b). si f(a) = f(b), entonces hay al menos un número c en (a, b) donde f’(c) = 0.

    Podemos confirmar este teorema usando el teorema de la continuidad presentado en la pasada publicación. En este vimos que una función continua podemos encontrar un máximo o mínimo absoluto en tres escenarios posibles. 

1. puntos interiores donde ƒ' = 0.
2. puntos interiores donde ƒ' es indefinido.
3. puntos finales del dominio de ƒ.

    Como f es diferenciable en cada punto interior por definición podemos excluir el escenario 2 dejándonos así el escenario 1 y 3.

    En el caso del escenario 1 si un máximo o mínimo ocurre en el punto c entre a y b entonces f’(c) = 0 por lo tanto hemos encontrado un punto que valida el teorema de Rolle.

    Si tanto el máximo absoluto como el mínimo absoluto ocurren en los extremos entonces debido a que f(a) = f(b) se da el caso que f es una función constante para cada x ∈ (a, b), por lo tanto f’(x) = 0 y el punto c se puede tomar en cualquier punto interior (a, b) cumpliendo así el escenario 3. Esto forma nuestro primer corolario.

    Corolario 1. Si f’(x) = 0 en cada punto x de un intervalo abierto (a, b), entonces f(x) = C para todas x ∈ (a, b), donde C es una constante.

    ¿Pueden existir funciones complicadas cuyas derivadas siempre sean igual a cero? La respuesta según este corolario es que solo las funciones constantes tienen una derivada igual a cero.

    La prueba de este teorema es esencial ya que si esta falla aunque sea en un punto su grafica puede no tener una tangente horizontal, pero ¿por qué es importante tener esta tangente? De esto es que trata el teorema del valor medio.

    El Teorema del Valor Medio es una propiedad de las funciones derivables en un intervalo. Considerado como el teorema más importante del cálculo. Una forma mas restringida de este fue demostrada por Michel Rolle en 1691 para polinomios sin la técnica de cálculos y hoy es conocida como el teorema de Rolle que acabamos de comprobar. El teorema del valor medio postula lo siguiente.

• Si f es una función continua en el intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b) tal que la tangente en el punto c es paralela a la recta secante en los puntos (a, f(a)) y (b, f(b)), en lenguaje geométrico es fácil de formular y entender como se muestra a continuación.

    Prueba. imaginamos el gráfico f y dibujamos una línea a través de los puntos A (a, f(a)) y B (b, f(b)). La función de la línea la podemos representar usando la ecuación de la pendiente.

    La diferencia vertical entre las gráficas f y g la representamos con la función h(x).

    La función h satisface la hipótesis del teorema de Rolle en [a, b]; es continua en [a, b] y diferenciable en (a, b) pues f y g lo son. También h(a) = h(b) = 0 por lo tanto existe un h’(c) = 0 en un punto c ∈ (a, b). Este es el punto que deseamos para la ecuación, para ello vamos a diferenciar ambos lados con respecto a x y luego establecer x = c.

Cuando h’(c) = 0

    Esto también confirma que el teorema de Rolle es una versión mas restringida de lo que es el teorema del valor medio.

    Ejemplo. La función f(x) = x² es continua de 0 ≤ x ≤ 2 y diferenciable en 0 < x < 2 como f (0) = 0 y f (2) = 4, el teorema del valor medio nos dice que existe un punto c en este intervalo donde la derivada f’(x) = 2x, debe tener un valor de (4-0) / (2-0) = 2. En este caso encontramos el valor de c resolviendo la ecuación 2c = 2 que nos da c = 1.

    ¿Qué tal si queremos saber la relación entre dos funciones que tienen la misma derivada en un intervalo determinado?

    Existe un segundo corolario que nos dice que sus valores se diferencian por una constante.

    Corolario 2. Si f’(x) = g’(x) en cada punto x de un intervalo abierto (a, b), entonces existe una constante C tal que f(x) = g(x) + C para todas x ∈ (a, b). Eso es f – g es una función constante en (a, b).

    Dos funciones pueden tener la misma derivada pero no necesariamente ser iguales. Estas difieren en una constante.

    El teorema del valor medio es de mucha importancia para la siguiente sección de calculo que trataremos. También ha sido utilizada para comprobar las leyes logarítmicas y exponenciales. Aquí debajo les presentare un ejemplo de estas y con esa idea ustedes pueden intentar probar las demás leyes.

    Prueba que ln(bx) = ln(b) + ln(x).

    El argumento comienza observando que ln(b) y ln(x) tienen la misma derivada.

    Acorde a nuestro segundo corolario las funciones difieren por una constante, lo que significa que

    ya que esta ecuación se mantiene para todos los valores positivos de x, debe mantenerse para x = 1. Por lo tanto,

    Ahora podemos sustituir y ver 

    Comprueba que 

    Sea y₁ = e^x₁ y y₂ = e^x₂, entonces tomando el logaritmo de ambos lados.

x₁ = lny₁ y x₂ = lny₂

x₁+x₂ = lny₁+lny₂ 

    Aplicando la regla de multiplicación de logaritmos

x₁+x₂ = lny₁y₂

    Exponenciándolos nuevamente

e^x₁^+x₂ = e ^lny₁^y₂

= y₁y₂ 

    Sustituyendo

e^x₁^+x₂ = e^x₁.e^x₂

 

Definición

• Corolario: Es una proposición que no necesita ser verificada, ya que se deduce muy fácilmente de lo demostrado.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

• Facebook: https://www.facebook.com/AprendeMatematicasJMD
• Twitter: @JMDciencias
• Correo: institutodecienciasjmd@hotmail.com

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

• Facebook: https://www.facebook.com/JMDFisica
• Blogger: jmdfisica.blogspot.com