En publicaciones anteriores analizamos métodos para integrar una variedad de funciones, uno de ellos es el método de sustitución y el teorema fundamental del cálculo. Este último nos dice cómo evaluar una integral definida usando antiderivadas. En la tabla 1 se presenta una versión resumida de lo que hemos estudiado hasta ahora.
 |
| Tabla 1. Integrales indefinidas previamente exploradas. |
Para
evaluar funciones más complicadas, crearemos otra técnica importante para
encontrar antiderivadas para muchas combinaciones de funciones.
Integración por partes
La
integración por pares es una técnica para simplificar integrales de la forma.
La técnica
es más útil cuando f se puede diferenciar repetidamente y g se
puede integrar repetidamente sin dificultad. Como cualquier otro método, el
propósito de la integración por partes es encontrar una expresión que sea más
simple que la integral dada.
Ej1. Encontrar ∫x cos(x)dx
Si
etiquetamos la función f(x) = x y g(x) = cos(x) encontramos que f(x)
se puede derivar repetidamente sin dificultad y se puede utilizar la
integración por partes. Funciones como ln(x), e x también
funcionan con el método de integración por partes. Ahora que sabemos qué tipo
de funciones se pueden usar, descubramos cómo usamos el método de integración
por partes. Comencemos usando la forma de diferenciación de la regla del
producto.
Si f y
g son funciones derivables de x, la regla del producto establece.
Donde f'(x)
y g'(x) son las derivadas df /dx y dg/dx.
En términos de integrales
indefinidas.
O
Reorganizando
Conduciendo
a la fórmula de integración por partes.
(1)
Si
consideras difícil recordar esta fórmula, también podemos escribirla en forma
diferencial usando sustitución u. Así lo aprendí y lo memoricé.
Sean u = f(x) y v = g(x) tales
que du = f'(x)dx y dv = g'(x)dx
Podemos reescribir la
ecuación 1.
(2)
El objetivo
de la integración por partes es pasar de una integral ∫ udv
que no sabemos
cómo evaluar a una integral ∫ vdu que sí podemos evaluar. Para que
este método sea más efectivo recomendamos elegir dv primero. Este debe
contener la mayor cantidad de integrando que puedas integrar. Tú serás
el sobrante.
Ej1. Encontrar
∫x cos(x)dx
Hay cuatro opciones disponibles para u y dv.
- Sea u = 1 y dv = x cos(x)dx
- Sea u = x y dv = cos(x)dx
- Sean u = x cos(x) y dv = dx
- Sea u = cos(x) y dv = xdx
Si elegimos 1 para integrar,
obtenemos du = 0 y dv es la función que estamos tratando de
encontrar, así que terminamos en el mismo lugar.
Si elegimos 3 para integrar,
entonces du = cos(x) – x sen(x) y dv = dx à v = x.
La nueva integral es incluso más
complicada que la anterior, por lo que no es una buena dirección para seguir.
La opción 4 tampoco es muy buena, por lo que nos queda la opción 2.
Si elegimos 2 para integrar;
u = x y dv = cos(x)dx à du = dx y v = sin(x).
Ahora
tenemos una expresión que satisface la condición y parece menos complicada que
la expresión anterior ya que ya no depende de la integración. Encontrar una
expresión más simple no siempre es intuitivo y la elección de u y dv afectará
el resultado, como vimos en el ejemplo 1. Recomiendo elegir una u cuya
derivada se haga más pequeña o simple, y una dv cuya antiderivada estes
muy familiarizada. Se ha propuesto una regla general que consiste en elegir
como u la función que aparece en primer lugar en la siguiente lista.
L – función logarítmica.
I – función trigonométrica
inversa (incluido el análogo hiperbólico).
A – funciones algebraicas (polinomios).
T – funciones trigonométricas (incluidas las análogas hiperbólicas).
E – Exponenciales.
En nuestro
ejemplo 1 tenemos un polinomio antes de nuestra función trigonométrica, por lo
que seguir la regla de LIATE u = x es nuestra mejor opción, y se
demostró cuando resolvimos usando la opción 2.
En
ocasiones debemos utilizar la integración por partes más de una vez.
Ej2. Evaluar ∫ x2ex dx
Usando la
regla LIATE podemos elegir u = x2, dv = ex dx tal
que du = 2xdx y v = ex
La nueva
integral es menos complicada que la original, pero aún tenemos que resolverla,
así que apliquemos la integración por partes nuevamente con u = x, dx
= ex dx luego du = dx , v = ex
Sumando todo obtenemos.
Esta
técnica funciona para cualquier integral ∫ xn ex dx donde n sea un número
entero positivo.
A veces, al
utilizar la integración por partes, podemos terminar regresando a la integral
original y sentirnos atrapados en un ciclo sin fin, pero en esos casos la
solución es bastante simple.
Ej3. Evaluar ∫ ex cos(x)dx
Usando
LIATE elegimos nuestro u = cos(x) y dv = ex dx, tal
que du = – sin(x)dx y v = ex.
Hay que
volver a aplicar la integración por partes.
U = sin(x); dv = ex dx à du = cos(x) dx; v = ex
La integral
desconocida ahora es la misma integral con la que empezamos. Ahora podemos
seguir bajando por la madriguera del conejo y usar la integración por partes
una y otra vez, pero esto demuestra que la integral está dando vueltas.
Afortunadamente, esta es una ecuación (verifique el signo de igualdad) y
podemos agrupar términos semejantes de manera que
Dividiendo
ambos lados por 2 obtenemos una solución para la integral desconocida.
Ej4. Resuelve ∫ cosn(x)dx para obtener una fórmula que exprese la integral donde n es un
número entero positivo.
En
problemas como este podemos usar algo llamado fórmula de reducción porque
reemplaza una integral que contiene alguna potencia de una función con una
integral de la misma forma con la potencia reducida. Para esto usaremos la
técnica de multiplicar por una expresión que sea igual a 1.
Comencemos
reescribiendo la función.
Podemos
hacer esto porque la expresión básicamente se multiplica por 1. Esta
nueva expresión tiene su potencia reducida por lo que ahora podemos colocarla
en la integral y usar la integración por partes.
Dejar u
= cos n–1 (x) dv = cos(x) dx; du = (n – 1) cos n
–2 (x) (–sen(x)) dx; v = sin(x)
Podemos
usar una identidad trigonométrica para simplificar la expresión.
La integral
final es la integral original con la que comenzamos más el término extra (n
– 1), y sabemos qué hacer en estos casos.
Puede que
esta expresión no parezca bonita, pero es muy útil para resolver cualquier
integral de esta forma. Digamos
que n =2.
Evaluación de integrales definidas por partes
Podemos
usar la integración por partes para evaluar la integral definida en un límite
dado.
(3)
Normalmente
usamos la notación u y v porque es más fácil de recordar.
(4)
Ej5. Evaluar
Usando
LEITA u = x, dv = e– x dx ; du = dx y v = –e
–x entonces.
En el próximo post veremos más ejemplos de integración por partes.
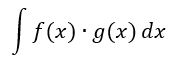


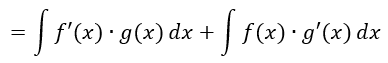








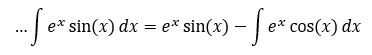











No hay comentarios.:
Publicar un comentario