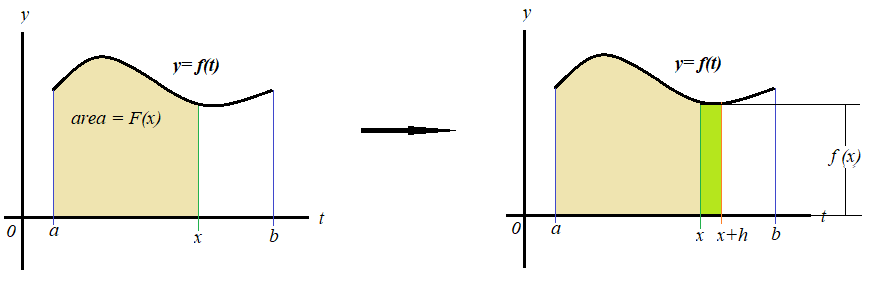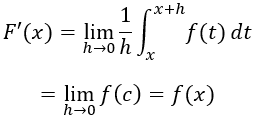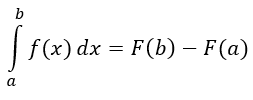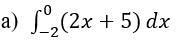Mas Ejemplos de Integrales.

     Vamos a trabajar algunos ejercicios para ver las propiedades que aprendimos en la pasada publicación.

Evalúa las integrales.

    Este es un ejercicio bastante directo. Primero debemos hacer una sustitución que permita la simplificación del ejercicio y luego evaluar la sustitución en los límites para obtener nuevos límites. Recordemos que la raíz cuadrada es igual que la potencia ½. Para nuestra sustitución elegí.

• Sea u = y + 1 à du = dy
• Cuando y = 0, u = 1
• Cuando y = 3, u = 4

Nuestra sustitución será. 

    En este caso la sustitución añade un término extra así que debemos ser cuidadoso con eso.

• Sea u = 1 + t⁴ à du = 4t³ dt; ¼ du = t³ dt
• Cuando t = 0, u = 1
• Cuando t = 1, u = 2

    La sustitución hizo de este problema algo bastante simple. Otro método que podíamos utilizar fue el de la distribución de potencial y luego evaluar la integral para cada termino. La integral a evaluar seria la siguiente.

t³(1 + t⁴)³ = t³(1 + 3t⁴ + 3t⁸ + t¹²)

= t¹⁵ + 3t¹¹ + 3t⁷ + t³

    For this problem the important fact to remember is that the denominator is simply a negative exponential.

• Sea u = 4 + r² à du 2r dr; ½ du = r dr
• Cuando r = 0, u = 4
• Cuando r = 1, u = 5

• Sea u = 1 – cos (3t) à du = 3sin (3t) dt; 1/3 du = sin (3t) dt
• Cuando t = 0, u = 0
• Cuando t = π/6, u = 1

Encuentra el área de la región sombreada.

    Los siguientes ejercicios tratan sobre el análisis grafico para determinar las propiedades que necesitamos para calcular áreas usando integrales. Para ello necesitamos conocer la función que compone el área sombreada y los limites tanto del eje x como del eje y ya que no sabemos cual de los dos ejes nos facilitara la integral.

    Tenemos que la función es descrita en términos de x así que evaluaremos esta integral con respecto a x. los límites de integración con respecto a x son – 2 < x < 2 lo que lo hace un intervalo simétrico Antes de tratar de resolver voy a confirmar si la función es par o impar. Ya que los límites de integración satisfacen la condición de simetría. 

    La función es impar por lo que la integral debe ser cero. Esto también lo podemos apreciar al ver la gráfica ya que el área de la función es como un reflejo de si misma. Vamos a confirmarlo.

• Sea u = 4 – x2 à du = – 2x dx; – ½ du = x dx

    Este caso es bastante directo, tenemos una función definida en términos de x y su intervalo es – π < x < 0. Si hay algo que nos puede servir para solucionar este problema es el conocimiento de que el seno es una función impar y el coseno es una función par, es decir sin (–x) = – sin (x); cos (–x) = cos (x).

• Sea u = 1+ cos x à du = – sin x dx; – du = sin x dx

    In this case we can rewrite the functions to integrate with respect to x, but it will be easier to Integrate with respect to y instead. El intervalo de las funciones va 0 < y < 1 y como estamos usando el eje y el orden de las funciones va de derecha a izquierda, obtenemos f(y) = 12y² – 12y³ y g(y) = 2y² – 2y.

 

    Podemos integrar esta área usando el eje x. de arriba hacia abajo tenemos que f(x) = 1 y g(x) = cos² x y los límites de integración a = 0 y b = π.

    Para resolver este problema utilizaremos dos identidades trigonométricas para simplificar el problema.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

• Facebook: https://www.facebook.com/AprendeMatematicasJMD
• Twitter: @JMDciencias
• Correo: institutodecienciasjmd@hotmail.com

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

• Facebook: https://www.facebook.com/JMDFisica
• Blogger: jmdfisica.blogspot.com

Teorema Fundamental del Calculo

    El Teorema fundamental del cálculo es un teorema que conecta la integración y la diferenciación, lo que nos permite calcular integrales utilizando una antiderivada de la función del integrando en lugar de tomar los límites de las sumas de Riemann.

    Este teorema se compone de dos partes: la primera parte implica la existencia de antiderivadas para funciones continuas, mientras que la segunda parte nos permite encontrar antiderivadas por integración simbólica evitando la integración numérica.

    Tomar los límites de las sumas de Riemann es un proceso largo y, dependiendo de la función, puede volverse muy difícil de calcular, por lo que fue necesario desarrollar un método más poderoso para evaluar integrales definidas. Este nuevo método se basará en el uso de antiderivadas. Este método combina las dos posiciones del cálculo que hemos estudiado hasta ahora (tomando los límites de sumas finitas para obtener una integral definida y el uso de derivadas y antiderivadas).

Parte 1

    Si f(t) es una función integrable en un intervalo finito I, entonces la integral f en cualquier número fijo x ∈ I a otro número a ∈ I define una nueva función F cuyo valor en x es

(1)

(las funciones f(x) y F(x) son diferentes).

    La importancia de esta nueva función radica en la conexión que hace entre integrales y derivadas.

    Veamos la geometría detrás de esto para ver cómo se mantiene este resultado.

    Sea f(x) ≥ 0 en [a, b], entonces F'(x) se puede calcular usando la definición de la derivada y tomando el límite como h à 0 del cociente de diferencias.

    Si h es pequeña, esta área es aproximadamente igual al área del rectángulo de altura f(x) y ancho h.

Dividiendo ambos lados por h à 0 obtenemos.

    Este resultado forma la primera parte del Teorema Fundamental del Cálculo.

• Si f es continua en [a, b], entonces  es continua en [a, b] y derivable en (a, b) y su derivada es f(x). 

(2)

    Básicamente, el teorema nos dice que, si F es la antiderivada de f, entonces la derivada de F es igual a f porque la derivada de la antiderivada te dará la función original. podemos comprobar esto utilizando el conocimiento que hemos recopilado hasta ahora. Comencemos usando la definición de derivada.

    Esto podemos reescribirlo usando la propiedad de aditividad que vimos en la publicación pasada.

    Según el teorema del valor medio, el valor antes de tomar el límite es uno de los valores que toma f entre x y x+h, es decir, para algún número c en este intervalo.

    Cuando h à 0, x+h se aproxima a x forzando a c a aproximarse también a x (porque c está atrapada entre x y x+h).

En conclusión.

    Esto es cierto incluso para x = a o b, ya que se convierte en un límite unilateral con h à o⁺ o h à o^- respectivamente. Veamos algunos ejemplos.

    Usando el teorema fundamental del cálculo para encontrar dy/dx.

    Este primer ejemplo es muy simple ya que esta formulado directamente como lo indica el teorema así que solo hacemos una sustitución de variable t por x en la función.

    Este ejemplo tiene algo diferente y es que los valores de la integración están invertidos así que debemos colocarlos en el orden parecido al presentado en el teorema. Para ello podemos utilizar propiedad de integración que vimos en la publicación pasada.

    Este ejemplo es muy diferente a los dos previos ya que tenemos que el límite de integración no es x sino x² haciendo que y sea una función compuesta de las dos variables. Para resolver esto debemos usar sustitución y la regla en cadena de la derivación.

Sustituimos x² = u à du/dx = 2x

Aplicamos la regla en cadena  .

    En este ultimo ejemplo debemos aplicar todas las diferentes variedades que utilizamos en los ejemplos anteriores. Empecemos reorganizando los puntos extremos de la integral.

Ahora aplicamos sustitución. v = 2+3x² à dv/dx = 6x

Finalmente aplicamos la regla en cadena  .

Parte 2

    La segunda parte del teorema describe cómo evaluar integrales definidas utilizando antiderivadas en los límites superior e inferior en lugar de calcular los límites de las sumas de Riemann.

• Si f es continua en todo punto en [a, b] y F es cualquier antiderivada de f en [a, b], entonces.

(3)

    El teorema de evaluación es importante porque nos dice que para calcular la integral definida necesitamos hacer dos cosas:

1. Encuentre una antiderivada de la función.
2. Evalúe la antiderivada en los extremos (a, b) de modo que el número F(b) - F(a) sea igual .

    Este proceso es mucho más fácil que usar el cálculo de sumas de Riemann. La notación usual para la diferencia F(b) - F(a) es.

    Dependiendo del número de términos que tenga F. Veamos algunos ejemplos.

    Usando la parte 2 del teorema fundamental del cálculo evalué las siguientes integrales.

    Nuestro primer ejemplo es simple, y para encontrar su antiderivada podemos usar la tabla de reglas de la publicación de antiderivadas para obtener lo siguiente.

    Es importante estar atento a los signos. La mayoría de los errores en matemáticas son asociados a estos pues nos sentidos tan cómodos con ellos que fácilmente los omitimos y cometemos errores.

    Esta función se ve un poco intimidante, pero usando nuestras propiedades podemos dividirlas en partes y hacer que su cálculo mucho más fácil.

    Ahora tenemos dos integrales donde la primera es bastante simple de computar mientras que en la segunda podemos usar una de las propiedades trigonométricas para resolver una función mas simple o puedo sustituir la variable por una mas simple.

Sea x = 2t à dx = 2 dt. Así que dt = ½ dx.

Empecemos simplificando la expresión.

    Elegí representarlo de esta forma para que se haga obvio como calcular la antiderivada.

    Como se puede ver si trabajamos con antiderivadas el problema de integración se resuelve en unas cuantas líneas de computación haciendo del problema algo más fácil de manejar. En la próxima publicación voy a expandir el método de sustitución al igual que las integrales indefinidas. También estaré tocando las funciones inversas trigonométricas para ver como son representadas en una derivada y una integral.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

• Facebook: https://www.facebook.com/AprendeMatematicasJMD
• Twitter: @JMDciencias
• Correo: institutodecienciasjmd@hotmail.com

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

• Facebook: https://www.facebook.com/JMDFisica
• Blogger: jmdfisica.blogspot.com