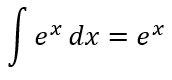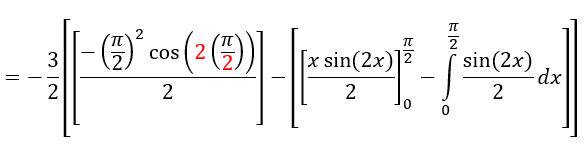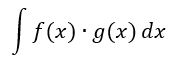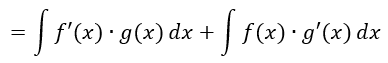Evalúa las siguientes integrales.
Para poder
resolver esta integral tendremos que utilizar dos métodos. El método de u sustitución e integración por
partes. Usemos letras diferentes para no confundir sustitución de u con
integración por partes.
Sea t = πθ àdt = π dθ ; 1 /
π du = dθ
Sea u = t à du = dt; dv = cos(t) dt à v = sin(t)
Si usamos LIATE obtenemos u = ln(x) à du = 1/x dx; dv = xdx à v = ½ x 2 . También te recomiendo que en cada apartado que resuelvas la integral la evalúes, de esa manera podrás llevar un registro de los valores de la respuesta.
La forma
más sencilla que considero de evaluar esta integral es dividirla en varias
integrales y evaluar cada una individualmente.
Usando
integración por partes evaluamos la primera integral. Sea u = x 2 à du = 2x; dv = e x dx à v = e x.
Volvamos a
la integración por partes. Curiosamente, la integral que resolveremos es
también la segunda integral que tendremos que resolver más adelante, por lo que
esto facilitará las cosas.
Sea u = 2x
à du
= 2dx; dv = e x dx à v = e x
También es
la solución de nuestra siguiente integral, por lo que solo nos falta la
integral final.
Ahora
debemos juntarlo todo y simplificarlo.
Tenemos
que volver a aplicar la integración por partes. Sea u = sin(y) àdu = cos(y) dy ; dv = e–y dy
à v = –e–y
Como en la
publicación anterior, podemos terminar con la integral original para poder usar
las propiedades de la ecuación y llevarla al otro lado.
Para
resolver este caso primero debemos usar la sustitución u y luego
descubriremos algo interesante. Para evitar confusiones con la integración por
partes, utilizaré una letra diferente. Sea t = 2xà dt = 2dx entonces ½ dt = dx.
Esta
integral es similar al problema anterior con un seno en lugar de un coseno.
Entonces nuestra respuesta será similar, pero con un cambio de signo y un ½
término extra (si no estás seguro de por qué puedo hacer esta afirmación, busca las propiedades derivadas del seno y el coseno como funciones pares e impares).
Ahora
bien, este problema parece muy complicado, pero en realidad es muy simple. De hecho,
no necesitamos utilizar la integración por partes para resolver. Preferiríamos
utilizar la sustitución u para facilitar mucho el problema.
Sea u =
x 2 àdu = 2xdx; ½ du = xdx
Si te
preguntas cómo encontré la integral para esta función trigonométrica, me
expandiré más en la próxima publicación cuando tratemos la integración de
funciones trigonométricas.
En este
caso necesitamos usar la integración por partes y para simplificar el cálculo,
también usaré una identidad trigonométrica para cambiar mi expresión hacia algo
más manejable. Sea u = x àdu = dx; dv = tan 2 (x)dx;
¿v =? para
encontrar la primitiva de tan 2 (x) sustituiré la función por una
identidad.
Si lees mi
post sobre “antiderivadas” podrás encontrar la antiderivada
de la sec2 (x) que es tan(x), quedando así la
antiderivada de tan2(x) = tan(x) – x y esta es v.
Al evaluar
la integral a medida que avanzamos evitamos agrupar el problema, lo que a su
vez simplifica las cosas.
El valor
de tan (π/3) y sec(π/3) no es fácil de encontrar.
Generalmente la gente memoriza estos valores o usa una calculadora, en mi caso
tengo una tabla diseñada con los valores comunes para los ángulos más comunes.
Si alguien está interesado, hágamelo saber y puedo compartirlo en una
publicación o en la sección de comentarios.
Mantengamos
la tendencia y usemos la integración por partes en este caso. Sea u = x àdu = dx; dv = √ (1 – x). para una mejor comprensión se
puede reescribir como dv = (1 – x) ½ dx à v = –2/3 (1 – x) 3/2. Para este caso voy a encontrar la
solución completa de la integral y luego la evaluaré para ver cómo se compara
con la anterior.
Ahora
podemos evaluar.
Esta
integral requerirá que integremos varias veces, por lo que es mejor evaluar a
medida que avanzamos para evitar saturar nuestro problema. Por supuesto, eso
depende de la persona que resuelve el problema. Si te sientes más cómodo
resolviendo todo al final también es bueno.
Sea u =
x3 à du = 3x2dx; dv = cos(2x)dx à v = sin(2x)/2
Apliquemos
nuevamente la integración por partes. Tenga en cuenta que sin(π) = 0 y cos(π) = –1.
Sea u =
x2 à du = 2xdx; dv = sin(2x) dx à v = –cos(2x)/2
Una vez
más aplicamos la integración por partes.
Sea u = x à du = dx; dv = cos(2x) dx à v = sin(2x)/2
La
integral final es fácil de evaluar y no necesitamos aplicar la integración por
partes. Así que finalmente podemos resolver todo.
Este es
otro problema que parece intimidante, pero es bastante simple. No necesitamos
usar la integración por partes porque la sustitución en u la simplificará.
Sea u = √x
à du = ½
(x) –½ dx tal
que 2du = dx/√x