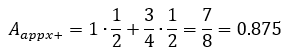Integrales parte 1 (actualizada)

Estimación de áreas

    En pasadas publicaciones tratamos el tema de “áreas y perímetros”. Para figuras geométricas regulares determinar el área es un proceso bastante simple. Existen fórmulas directas que nos permite determinar este valor (el área de un triángulo es igual a la mitad de su base multiplicada por su altura), pero cuando tenemos figuras geométricas irregulares determinar el área es un proceso más complejo.

    Existen figuras irregulares que podemos conocer su área si la dividimos en secciones y sumamos sus partes,

    En la figura de arriba vemos que podemos partir esta imagen en tres regiones y calcular de esta forma su área total.

    Sin embargo, no todas las figuras irregulares las podemos examinar como estas. Existen figuras que no podemos calcular usando esta técnica o simplemente no tenemos la información suficiente.

    En este caso tenemos una función f(x) dada y queremos determinar el área debajo de la curva de la función en el intervalo (a, b). Determinar el área de esta función dependerá del tipo de función que sea f(x), por lo que este problema se puede hacer bastante complicado usando solamente algebra. Por el resto de esta publicación vamos a trabajar una técnica para aproximar el área de funciones como esta. Esta técnica es importante para el desarrollo de la teoría de integración. Vamos a empezar considerando un ejemplo numérico y de esta vamos a extraer las características esenciales para crear nuestra teoría.

    Supongamos que queremos conocer el área de la región sombreada creada por una función y = 1- x² en el intervalo x = 0 hasta x = 1. En este tipo de casos no existe un método algebraico especifico ni formula que se pueda usar para calcular el área exacta, pero si podemos aproximarla usando un método bastante simple. Podemos tomar nuestra área sombreada y dividirla en regiones usando rectángulos para calcular la aproximación del área. Si decidimos dividir la figura en dos rectángulos entonces tendremos rectángulos con una anchura de 0.5 y su altura dependerá de su ubicación (el valor de x nos permite conocer el valor de y en la ecuación).

    Su área aproximada es la suma de estas dos regiones.

    Esta estimación es mayor que el área real A, ya que los dos rectángulos contienen regiones fuera de la parte sombreada, y esto se suma a la cantidad calculada. decimos que esta es una suma superior porque se obtiene tomando la altura de cada rectángulo como el valor máximo (superior) de la función. Si analizamos la función de izquierda a derecha, tenemos nuestro primer punto donde toca la gráfica y nos movemos hacia la derecha hasta nuestro segundo punto donde toca la gráfica y nos movemos a la derecha otra al siguiente punto y así sucesivamente. De esta manera creamos una suma superior.

    Supongamos que usamos cuatro rectángulos contenidos dentro de la región para estimar el área.

    Esta estimación es más pequeña que el área A ya que todos los rectángulos se encuentran dentro de la región. La suma de estos rectángulos con alturas iguales al valor mínimo de la función se denomina aproximación de suma inferior. En este caso analizamos la figura de derecha a izquierda; el primer punto donde toca la grafica y nos movemos a la izquierda hasta el próximo punto y subimos hasta donde toca la grafica y nos movemos de nuevo a la izquierda hasta el siguiente y subimos donde toca la gráfica y así continuamente.

    No siempre vamos a obtener una suma inferior si nos movemos de derecha a izquierda ni una superior si nos movemos de izquierda a derecha, la es que si calculamos desde el punto mas alto de la gráfica hasta el más pequeño entonces tendremos una suma superior y si contamos desde el punto más pequeño de la grafica hasta el punto mas alto entonces tendremos una suma inferior.

    Al considerar las aproximaciones de suma inferior y superior, no solo obtenemos estimaciones para el área, sino también un límite en el tamaño del posible error en estas estimaciones, ya que el valor real del área se encuentra en algún lugar entre ellos. También obtenemos una mejor aproximación del área al tomar el promedio A_avg de la suma superior y la suma inferior.

    Si analizamos de forma abstracta podemos decir que, en cada una de nuestras sumas calculadas, el intervalo [a, b] sobre el cual se define la función f se subdividió en n subintervalos de igual ancho determinado por ∆x = (b - a)/n y f se evaluó en un punto de cada subintervalo: c₁ en el primer subintervalo, c₂ en el segundo subintervalo, y así sucesivamente. Entonces todas las sumas finitas del área toman la forma.

    Las opciones para c_n podrían maximizar o minimizar el valor de f. Al tomar más y más rectángulos, con cada rectángulo más delgado que antes, parece que estas sumas finitas dan aproximaciones cada vez mejores y cercas al área real. Como el propósito es estar tan cerca del área real como sea posible, el número de rectángulos en el que vamos a dividir nuestra función no será tan simple como tener dos o tres rectángulos, de hecho, estamos hablando de una suma con muchos términos, por lo que escribir todos los términos uno por uno seria una tarea tediosa y hasta imposible si el número de términos es muy grande, pero las matemáticas tienen su propio lenguaje para expresar sumas de cantidades exorbitantemente grandes.

    La notación sigma nos permite escribir una suma con muchos términos en forma compacta.

    La letra griega ∑ (sigma mayúscula correspondiente a la letra S del alfabeto castellano), significa "suma". El índice en el número debajo del símbolo de suma k nos dice dónde comienza la suma y el número de arriba dónde termina.

Ejemplo.

Propiedades y reglas de sumas finitas.

• Regla de la suma

• Regla de la resta

• Regla de multiplicación por una constante

Cualquier valor de c

• Regla de valor constante 

c es cualquier valor constante

    Por ahora esto ha sido todo. En nuestra próxima publicación continuaremos con el tema usando el mismo ejemplo para calcular su area real. Es bueno tratar este tema despacio ya que es importante que entiendan cada paso si quieren comprender como funcionan las integrales. Si les gusto el tema por favor compartirlo y si tienen sugerencias por favor agregarlo en los comentarios.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

• Facebook: https://www.facebook.com/AprendeMatematicasJMD
• Twitter: @JMDciencias
• Correo: institutodecienciasjmd@hotmail.com

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

• Facebook: https://www.facebook.com/JMDFisica
• Blogger: jmdfisica.blogspot.com