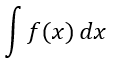Hemos
estudiado cómo calcular la derivada de una función, pero qué pasa si queremos
saber la función de una derivada dada. En términos propios, diremos que si f
es una función, queremos encontrar una función F cuya derivada sea f.
si existe la función F, la llamamos la antiderivada de la función f,
y este es el vínculo que conecta derivadas e integrales en cálculo.
- Una función F es una antiderivada de f en un intervalo abierto I si F’(x) = f(x) para todo x en I.
El proceso
de encontrar una antiderivada requiere que pensemos al revés, pero hay
derivadas simples que con solo mirarlas podemos identificar su antiderivada.
Ejemplo 1. Funciones y antiderivadas.
f(x) = 2x à F(x) = x2 g(x) = cos(x) à G(x) = sin(x) h(x) = 1/x à H(x) = ln |x|
Podemos
comprobar las respuestas diferenciando F(x), G(x) y H(x) y
ver si obtenemos f(x), g(x) y h(x) de regreso. Sin
embargo, estas soluciones no son únicas, existen otras funciones que pueden
proporcionar la misma función derivada, como x2 + 1 ó x2
+ C para cualquier constante C. uno de los corolarios del Teorema
del valor medio nos dice dos (funciones) antiderivadas cualesquiera difieren
por una constante. Esto nos permite crear un nuevo teorema para las
antiderivadas.
- Si F es una antiderivada de f en un intervalo I, entonces la antiderivada más general de f en I es
F(x) + C
(1)
la antiderivada más general de ƒ
sobre I es una familia de funciones cuyas gráficas son traslaciones
verticales unas de otras.
Ejemplo 2. Encuentra la antiderivada de f(x) = 3x2.
Como la derivada de x3
es 3x2, la antiderivada general es
F(x) = x3 + C
El valor de la constante se puede
encontrar usando condiciones especiales como las condiciones iniciales. en el
ejemplo 2 si queremos que la antiderivada satisfaga F(1) = –1.
F(1) = (1)3 + C = –1
1 + C = –1
C = –2
Por lo tanto la antiderivada de la función 3x2
que satisface F(1) = –1 es.
F(x) = x3– 2
Al trabajar hacia atrás, podemos
derivar fórmulas y reglas para antiderivadas, pero hacer esto requerirá mucho
tiempo para examinar múltiples casos y encontrar patrones. Afortunadamente para
nosotros, esto ya se ha hecho, así que solo necesitamos memorizar y aprender a
trabajar con ellos. Algunas de las reglas más generales para antiderivadas son
estas.
Integral
El conjunto de todas las antiderivadas de f
se llama integral indefinida y se denota por.
(2)
El
símbolo utilizado aquí es un signo integral, la función f es el
integrando y x es la variable de integración. Usando esta notación,
podemos reformular la solución del ejemplo 1 de la siguiente manera:
Esta notación se explorará más en nuestra
próxima serie de cálculo y es crucial en el desarrollo de lo que se conoce como
el Teorema Fundamental del Cálculo.
Ejemplo 3. Evaluar .
Podemos calcular cada antiderivada por
separado usando la tabla anterior.
Problema de Valor Inicial y Ecuaciones Diferenciales
Encontrar una
antiderivada es lo mismo que encontrar una función que satisfaga la ecuación.
(3)
A esto se le
llama ecuación diferencial. Para resolverlo necesitamos una función y(x)
que satisfaga la ecuación. Esta función se encuentra tomando la antiderivada de
f(x). la antiderivada más general.
F(x) + C
Da la solución
general de la ecuación diferencial y(x). Si se nos dan condiciones
especiales como
y(x0)
= y0
Eso
indica el estado inicial de la función, esto quiere decir que la función tiene
el valor y0 cuando x = x0. La combinación
de una ecuación diferencial y esta condición inicial se denomina problema de
valor inicial (PVI), y la solución a este problema son soluciones
particulares que satisfacen las condiciones iniciales. En el ejemplo 2, la
función y(x) = x3 – 2 es la solución particular de la
ecuación diferencial satisfaciendo
la condición inicial y(1) = –1. Este tipo de problemas se encuentran en
todas las ramas de la ciencia.
- Estudio del crecimiento y decadencia de la población.
- Absorción de glucosa por el cuerpo.
- Propagación de epidemias
- Segunda ley de movimiento de Newton
- Circuitos RL en electricidad
- Y mucho más.
El entendimiento de las antiderivadas se hace más fácil por medio de la practica así que aquí les dejo unos ejercicios para que practiquen y en la próxima publicación les presentare los resultados.
Encuentre
las antiderivadas de cada función.
- x2 - 2x + 1
- x-4 + 3x2 + 2
- x-3/2 + x2
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden seguir nuestro otro blog si les
interesa aprender sobre el interesante mundo de la física.
- Facebook: https://www.facebook.com/JMDFisica
- Blogger: jmdfisica.blogspot.com