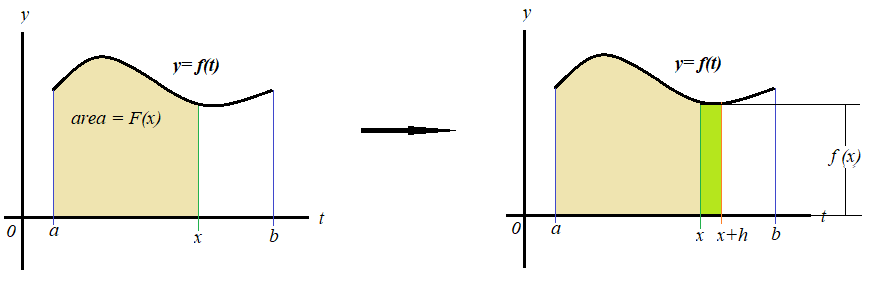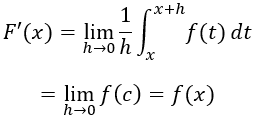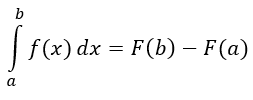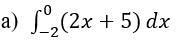Aprende Matemáticas JMD

martes, 12 de abril de 2022

Teorema Fundamental del Calculo

El Teorema fundamental del cálculo es un teorema que conecta la integración y la diferenciación, lo que nos permite calcular integrales utilizando una antiderivada de la función del integrando en lugar de tomar los límites de las sumas de Riemann.

Este teorema se compone de dos partes: la primera parte implica la existencia de antiderivadas para funciones continuas, mientras que la segunda parte nos permite encontrar antiderivadas por integración simbólica evitando la integración numérica.

Tomar los límites de las sumas de Riemann es un proceso largo y, dependiendo de la función, puede volverse muy difícil de calcular, por lo que fue necesario desarrollar un método más poderoso para evaluar integrales definidas. Este nuevo método se basará en el uso de antiderivadas. Este método combina las dos posiciones del cálculo que hemos estudiado hasta ahora (tomando los límites de sumas finitas para obtener una integral definida y el uso de derivadas y antiderivadas).

Parte 1

Si f(t) es una función integrable en un intervalo finito I, entonces la integral f en cualquier número fijo x ∈ I a otro número a ∈ I define una nueva función F cuyo valor en x es

(1)

(las funciones f(x) y F(x) son diferentes).

La importancia de esta nueva función radica en la conexión que hace entre integrales y derivadas.

Veamos la geometría detrás de esto para ver cómo se mantiene este resultado.

Sea f(x) ≥ 0 en [a, b], entonces F'(x) se puede calcular usando la definición de la derivada y tomando el límite como h à 0 del cociente de diferencias.

Si h es pequeña, esta área es aproximadamente igual al área del rectángulo de altura f(x) y ancho h.

Dividiendo ambos lados por h à 0 obtenemos.

Este resultado forma la primera parte del Teorema Fundamental del Cálculo.

Si f es continua en [a, b], entonces $F(x) = \int\limits_a^x {f(t)} dt$ es continua en [a, b] y derivable en (a, b) y su derivada es f(x).

(2)

Básicamente, el teorema nos dice que, si F es la antiderivada de f, entonces la derivada de F es igual a f porque la derivada de la antiderivada te dará la función original. podemos comprobar esto utilizando el conocimiento que hemos recopilado hasta ahora. Comencemos usando la definición de derivada.

Esto podemos reescribirlo usando la propiedad de aditividad que vimos en la publicación pasada.

Según el teorema del valor medio, el valor antes de tomar el límite es uno de los valores que toma f entre x y x+h, es decir, para algún número c en este intervalo.

Cuando h à 0, x+h se aproxima a x forzando a c a aproximarse también a x (porque c está atrapada entre x y x+h).

En conclusión.

Esto es cierto incluso para x = a o b, ya que se convierte en un límite unilateral con h à o⁺ o h à o^- respectivamente. Veamos algunos ejemplos.

Usando el teorema fundamental del cálculo para encontrar dy/dx.

Este primer ejemplo es muy simple ya que esta formulado directamente como lo indica el teorema así que solo hacemos una sustitución de variable t por x en la función.

Este ejemplo tiene algo diferente y es que los valores de la integración están invertidos así que debemos colocarlos en el orden parecido al presentado en el teorema. Para ello podemos utilizar propiedad de integración que vimos en la publicación pasada.

Este ejemplo es muy diferente a los dos previos ya que tenemos que el límite de integración no es x sino x²haciendo que y sea una función compuesta de las dos variables. Para resolver esto debemos usar sustitución y la regla en cadena de la derivación.

Sustituimos x²= u à du/dx = 2x

Aplicamos la regla en cadena $\frac{{dy}}{{dx}} = \frac{{dy}}{{du}} \cdot \frac{{du}}{{dx}}$ .

En este ultimo ejemplo debemos aplicar todas las diferentes variedades que utilizamos en los ejemplos anteriores. Empecemos reorganizando los puntos extremos de la integral.

Ahora aplicamos sustitución. v = 2+3x² à dv/dx = 6x

Finalmente aplicamos la regla en cadena $\frac{{dy}}{{dx}} = \frac{{dy}}{{dv}} \cdot \frac{{dv}}{{dx}}$ .

Parte 2

La segunda parte del teorema describe cómo evaluar integrales definidas utilizando antiderivadas en los límites superior e inferior en lugar de calcular los límites de las sumas de Riemann.

Si f es continua en todo punto en [a, b] y F es cualquier antiderivada de f en [a, b], entonces.

(3)

El teorema de evaluación es importante porque nos dice que para calcular la integral definida necesitamos hacer dos cosas:

Encuentre una antiderivada de la función.
Evalúe la antiderivada en los extremos (a, b) de modo que el número F(b) - F(a) sea igual $\int\limits_a^b {f(x)} dx$ .

Este proceso es mucho más fácil que usar el cálculo de sumas de Riemann. La notación usual para la diferencia F(b) - F(a) es.

Dependiendo del número de términos que tenga F. Veamos algunos ejemplos.

Usando la parte 2 del teorema fundamental del cálculo evalué las siguientes integrales.

Nuestro primer ejemplo es simple, y para encontrar su antiderivada podemos usar la tabla de reglas de la publicación de antiderivadas para obtener lo siguiente.

Es importante estar atento a los signos. La mayoría de los errores en matemáticas son asociados a estos pues nos sentidos tan cómodos con ellos que fácilmente los omitimos y cometemos errores.

Esta función se ve un poco intimidante, pero usando nuestras propiedades podemos dividirlas en partes y hacer que su cálculo mucho más fácil.

Ahora tenemos dos integrales donde la primera es bastante simple de computar mientras que en la segunda podemos usar una de las propiedades trigonométricas para resolver una función mas simple o puedo sustituir la variable por una mas simple.

Sea x = 2t à dx = 2 dt. Así que dt = ½ dx.

Empecemos simplificando la expresión.

Elegí representarlo de esta forma para que se haga obvio como calcular la antiderivada.

Como se puede ver si trabajamos con antiderivadas el problema de integración se resuelve en unas cuantas líneas de computación haciendo del problema algo más fácil de manejar. En la próxima publicación voy a expandir el método de sustitución al igual que las integrales indefinidas. También estaré tocando las funciones inversas trigonométricas para ver como son representadas en una derivada y una integral.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

Facebook: https://www.facebook.com/AprendeMatematicasJMD
Twitter: @JMDciencias
Correo: institutodecienciasjmd@hotmail.com

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física.

Facebook: https://www.facebook.com/JMDFisica
Blogger: jmdfisica.blogspot.com

martes, 15 de marzo de 2022

Integrales parte 2

Límites De Sumas Finitas

Las aproximaciones de suma finita que consideramos se volvieron más precisas a medida que aumentaba el número de términos y se reducían los anchos de los subintervalos, pero ¿qué sucede si consideramos un caso en el que el número de casos crece hasta el infinito y el valor del ancho se reduce a cero? En casos como este, donde los números que estamos considerando son infinitesimalmente pequeños o grandes, usamos los límites.

Tomando nuestro ejemplo de la semana pasada, podemos encontrar el valor límite de las aproximaciones de suma inferior al área de la región debajo del gráfico y arriba del intervalo [0, 1] en el eje x usando rectángulos de igual ancho cuyos anchos se acerquen a cero y cuyo número se acerca al infinito.

Podemos calcular una aproximación de suma menor usando n rectángulos de igual ancho ∆x = (1 – 0)/n y vemos lo que sucede cuando n à ∞ Comenzamos subdividiendo [0, 1] en n subintervalos de igual ancho

Cada subintervalo tiene un ancho de 1/n. La función y = 1 – x² es decreciente en [0, 1], y su valor más pequeño en un subintervalo ocurre en el extremo derecho del subintervalo. Entonces, se construye una suma menor con rectángulos cuya altura sobre el subintervalo $\left[ {\frac{{k - 1}}{n},\frac{k}{n}} \right]$ es f(k/n) = 1 - (k/n)² dando la suma

Reescribiendo en notación sigma

Ahora podemos simplificar este problema aplicando algunas de las propiedades de las sumas finitas

Aplicamos la regla de la resta y como 1/n es solo una constante, aplicamos las propiedades de valor y múltiplo constantes. Ahora, la suma restante es simplemente una suma de los primeros n cuadrados, que es una suma especial que se está reescribiendo, así como la suma de los primeros n cubos.

Los primeros n cuadrados

Los primeros n cubos

Y si desean ver la derivación de esta fórmula, puedo crear una publicación adicional esta semana, pero deben informarme en sus comentarios. Mientras tanto, continuemos con nuestro ejercicio.

Ahora tenemos una expresión para la suma inferior que vale para cualquier n. todo lo que nos queda por hacer es evaluar el límite como n à ∞ y ver si la suma converge.

Aplicando algunas propiedades de los límites lo dividimos en secciones para un mejor análisis.

El límite como n à ∞ de 1/n es cero. Entonces, estos términos se cancelan.

Las aproximaciones de suma inferior convergen a 2/3. Un cálculo similar muestra que las aproximaciones de la suma superior también convergen a 2/3. Cualquier aproximación de suma finita también converge al mismo valor 2/3.

Sumas De Riemann

La teoría de los límites de las aproximaciones finitas fue precisada por el matemático alemán Bernhard Riemann utilizando lo que hoy se conoce como sumas de Riemann. esta teoría que subyace a la integral definida permite subdividir cualquier función arbitraria sobre un intervalo cerrado que puede tener valores positivos y negativos en subintervalos, no necesariamente de igual amplitud y formar sumas de la misma forma que para las aproximaciones finitas.

Comenzamos con una función acotada arbitraria ƒ definida en un intervalo cerrado [a, b]. Subdividimos el intervalo [a, b] en subintervalos, no necesariamente de igual ancho y formamos sumas de la misma forma que para las aproximaciones finitas, para ello elegimos n -1 puntos {x₁, x₂, x₃, …, x_n-1} que satisface

a < x₁ < x₂ < x₃ < … < x_n-1 < b

Si desea que la notación sea consistente, puede denotar a por x₀ y b por x_n.

a = x₀ < x₁ < x₂ < x₃ < … < x_n-1 < x_n = b

el conjunto

P = {x₀, x₁, x₂, x₃, …, x_n-1, x_n}

Se llama partición. La partición divide la región [a, b] en n subintervalos. En cada subintervalo seleccionamos algún punto. El punto elegido en el subintervalo k-ésimo se llama c_k. Luego, en cada subintervalo, colocamos un rectángulo vertical que se extiende desde el eje x para tocar la curva en (c_k, f(c_k)). En cada subintervalo formamos el producto f(c_k)∆x_k y finalmente sumamos todos estos productos.

Esta suma se llama suma de Riemann. La idea es que no importa cómo elijamos las particiones o los puntos c_k mientras las normas se acerquen a cero. Todas las opciones dan exactamente el mismo límite. Personalmente prefiero trabajar con particiones de igual ancho para simplificar mis cálculos, pero esto es una elección arbitraria, les recomiendo que si quieren mejorar practiquen estos ejemplos usando particiones de diferentes anchuras.

La Integral Definida

Sea f(x) una función definida en un intervalo cerrado [a, b]. decimos que J es la integral definida de f sobre [a, b] y que J es el límite de las sumas de Riemann si se cumple la siguiente condición:

Para cualquier número ϵ > 0 existe un número correspondiente δ > 0 tal que para cada partición P = {x₀, x₁, …, x_n} de [a, b] con norma ||P|| < δ y cualquier elección de c_k en [x_k-1, x_k] tenemos

Esta definición es muy técnica en lenguaje, pero básicamente lo que implica es un proceso limitante en el que la norma de la partición va a cero. El ancho está determinado por la diferencia entre los dos extremos, por lo que en el caso del primer subintervalo ∆x₁ = x₁ - x₀, y el ancho del segundo se denota por ∆x₂=x₂ - x₁, y así sucesivamente, pero en los casos en que todos los subintervalos tienen el mismo ancho, tenemos ∆x = (b – a)/n y la suma de Riemann se convierte en

Si el límite cuando n à ∞ existe y es igual a J, entonces J es la integral definida de f en el intervalo [a, b].

En el límite, el símbolo de la suma se reemplaza por el símbolo de la integral. Esta notación fue introducida por Leibniz. Los valores de la función f(c_k) se reemplazan por una selección continua de valores de la función f(x) y el ancho del subintervalo se convierte en el diferencial dx (recuerde que los pequeños cambios en el límite se representan como derivadas)

En nuestro ejemplo estamos evaluando la función 1 – x² en el intervalo [0, 1]. Podemos representarlo usando la notación integral como esta.

Su evaluación se hace usando las antiderivadas. Debemos encontrar la antiderivada de la función y luego evaluar en la diferencia de los puntos finales del intervalo. Para este caso las antiderivadas son fácil de encontrar.

En el caso del límite de la suma de Riemann, lo representamos como

Donde debemos elegir una partición para el intervalo si queremos resolverlo. Puedo elegir una partición de igual ancho para todos y usar la ecuación ∆x = (b – a)/n donde a y b son los extremos así que obtengo.

Entonces mi partición será

Ahora elijo un punto c_k basada en el ancho que es 1/n en cada sección. Así que tengo c_k = k/n

Con manipulación algebraica tenemos la siguiente expresión

Esto es exactamente lo mismo que obtuvimos cuando calculamos el límite de sumas finitas, por lo que su resultado será también el mismo. Indicando que este es el valor real del área.

Al definir $\int\limits_a^b {f(x)dx}$ como un límite de sumas $\sum\limits_{k = 1}^n {f\left( {{c_k}} \right)\Delta {x_k}}$ , nos movimos de izquierda a derecha a lo largo del intervalo [a, b]. pero si nos movemos de derecha a izquierda haciendo las mismas elecciones para cada punto, obtendremos el mismo resultado con un cambio de signo. por lo tanto, podemos concluir.

Orden de integración

Solo definimos la integral sobre un intervalo [a, b] cuando a < b, pero en el caso cuando a = b ese es el intervalo tiene ancho cero. Esto da ∆x = 0.

Intervalo de ancho cero

Tenemos otras propiedades que pueden ser útiles al evaluar funciones complicadas.

Múltiplo constante

Cualquier constante k

Suma y Resta

Aditividad

Desigualdad Max-Min

Si f tiene el valor máximo max f y el valor mínimo min f en [a. b], entonces

Dominación

Ejemplo. Calcule $\int\limits_0^b {x\,dx}$ y encuentre el área debajo de y = x sobre el intervalo [0, b], b > 0.

Si hacemos una gráfica de esta función, vemos que el área sombreada es un triángulo. Entonces, usando nuestras técnicas podemos calcular esta área de dos maneras con el límite de las sumas de Riemann y con la integral definida.

Usando el límite de las sumas de Riemann, debemos calcular para particiones cuya norma tiende a cero. Dado que no importa cómo elijamos nuestra partición, elegiré subintervalos de igual ancho por simplicidad.

Elegí c_k como el punto final derecho en cada intervalo y mi partición ahora se ve así.

Ahora podemos aplicar las propiedades que aprendimos de nuestra publicación anterior.

Tomando el límite cuando n à ∞ obtenemos

Este mismo resultado lo obtenemos si aplicamos el signo integral y sus técnicas.

Me disculpo por toda la teoría y el lenguaje técnico. Hice todo lo posible para simplificarlo lo más posible y hacerlo aceptable para los lectores. Básicamente, si desea poder usar el método de suma de Riemann, siga mis pasos en los ejemplos con cualquier función y luego intente usar el método integral y compare. Este tema me parece muy importante porque muestra cómo surgió la idea de la integración. Es importante aprenderlo en caso de que nos quedemos atascados con una antiderivada (ya que sinceramente no encuentro otro método que la memorización para aprenderlo) porque la suma de Riemann te permite trabajar cualquier función y llegar a su antiderivada básicamente.

Cualquier sugerencia por favor déjala en los comentarios, y si te gustó compártela con otras personas para que también puedan aprender de ella. En nuestra próxima publicación, hablaremos sobre el Teorema fundamental del cálculo y, con suerte, le agregaré algunos ejemplos.