Aplicación de la Integral Definida: Secciones Transversales

Una función continua sobre un intervalo cerrado tiene una integral definida. Esta integral se puede evaluar utilizando el Teorema Fundamental del Cálculo como vimos y demostramos en publicaciones anteriores. También demostramos que el área bajo una curva y el área entre dos curvas se pueden calcular usando integrales definidas. Ahora queremos extender el uso de integrales definidas para encontrar volúmenes, longitudes de curvas planas, áreas de superficies y, si es posible, ver su aplicación en algunas áreas de la física, como el trabajo realizado por una fuerza o la ubicación del centro de masa de un objeto. Todos estos procesos implican una aproximación por una suma de Riemann que al tomar el límite de esta se convierte en una integral definida.

Hallar volúmenes usando integrales y secciones transversales

El volumen es una medida tridimensional. Al multiplicar la altura, el ancho y la longitud, generalmente encontramos el volumen de una figura geométrica. Por el contrario, el área es bidimensional ocupando normalmente el largo y el ancho. Supongamos que queremos encontrar el volumen de un sólido S. Comenzamos extendiendo la definición de un cilindro de la geometría clásica a un sólido cilíndrico con bases arbitrarias. Si el cilindro sólido tiene un área base conocida A y una altura h, entonces el volumen es

Volumen = área x altura = A∙h

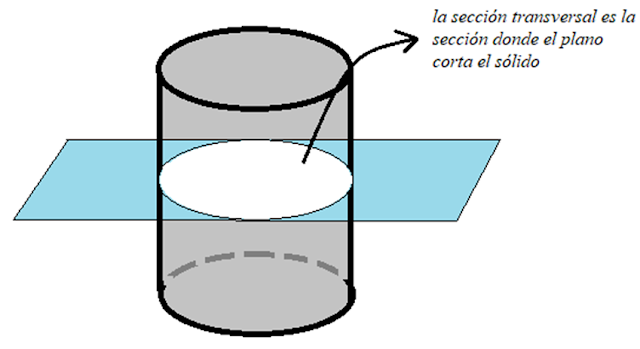
El área de la base se puede obtener mediante una sección transversal. Una sección transversal de un sólido es la región plana formada por la intersección del sólido con un plano (Figura 1). En esta publicación examinaremos tres métodos diferentes para obtener una sección transversal: el método de rebanado, el método del disco y el método de la arandela.

Figura 1. Plano cortando un cilindro creando asi una secion transversal.

Si la sección transversal del sólido S en cada punto x en el intervalo [a, b] es una región S(x) de área A(x), y A es una función continua de x, podemos definir y calcular el volumen del sólido como la integral definida de A(x).

Figura 2. 

Método de corte

En este método básicamente tomamos el intervalo y lo dividimos en subintervalos de ancho ∆x_k y cortamos el sólido como lo haríamos con una barra de pan por planos perpendiculares al eje x En los puntos a = x₀ < x₁ <… < x_n = b. los planos cortan el sólido S en losas delgadas, aproximamos la losa entre el plano en x_k-1 y el plano en x_k por un sólido cilíndrico con área de base A(x_k) y altura determinada por la distancia ∆xk = x_k – x_k–1. El volumen V_k es A(x_k)∙∆x_k el cual se aproxima al volumen de esa losa:

Volumen de la k-ésima losa = V_k ≈ A(x_k)∆x_k.

El volumen de todo el sólido se aproxima sumando todas las losas.

Figura 3.

Esta es una suma de Riemann para la función A(x) en [a, b]. ahora como tomamos el límite de las particiones de [a, b] que van a cero, tomamos el límite para encontrar su integral definida.

• El volumen de un sólido de área transversal integrable A(x) desde x = a hasta x = b es la integral de A desde a hasta b.

(1)

Para calcular el volumen de un sólido seguimos los siguientes pasos.

• Paso 1. Dibuje el sólido y una sección transversal típica. Si es posible graficar, hágalo ya que le dará una idea clara de lo que está calculando y cuáles serán los límites.
• Paso 2. Encuentra una fórmula del área de la sección transversal A(x). por lo general, las fórmulas para la sección transversal serán similares a las de un gráfico bidimensional. Si el sólido es muy complicado, podría dividirse en secciones más pequeñas para facilitar el cálculo de sus fórmulas.
• Paso 3. Encuentra los límites de integración. Esto se especificará o se encontrará como los puntos finales del sólido a lo largo del eje.
• Paso 4. Integre A(x) para encontrar el volumen. La función que integraremos es la que encontramos en la sección transversal. Este será el valor de A(x).

Ejemplo 1. Una pirámide de 5 m de altura tiene una base cuadrada de 3 m de lado. La sección transversal de la pirámide perpendicular a la altura x m desde el vértice es un cuadrado x m de lado. m significa metros, encuentra el volumen de la pirámide.

Paso 1. El enunciado nos dice que nuestro sólido será una pirámide y la sección transversal nos dice que su base será un cuadrado, entonces dibujamos su altura a lo largo del eje x y su vértice en el origen.

Figura 4. Piramide con base cuadrada alineada con el eje x.

Paso 2. La sección transversal es un cuadrado con un valor de x metros de lado por lo que su área es

A(x) = x²

Paso 3. Los límites de las integraciones están determinados por los extremos a lo largo del eje x. Dado que la altura de la pirámide se alineó arbitrariamente con el eje x, la longitud de la altura servirá como nuestros límites (esto no fue una coincidencia, se eligió deliberadamente de esa manera para simplificar los cálculos), por lo que los límites son de x = 0 a x = 5.

Paso 4. Pongamos todo junto en una buena expresión y calculemos el volumen.

El método del disco

Algunos sólidos se generan al rotar una región plana alrededor de un eje. Este método para calcular el volumen se llama método del disco porque la sección transversal es un disco circular de radio R(x), la distancia del límite de la región plana desde el eje de revolución es el área de la sección transversal. este dado por

A(x) = π(radius)² = π[R(x)]²

Porque es una revolución. Entonces, la definición de volumen en este caso

(2)

Ejemplo 2. Encuentra el volumen de la región entre la curva y = √x, 0 ≤ x ≤ 4 y gira alrededor del eje x.

Si creamos un gráfico de la función y = √x y luego giramos alrededor del eje x obtenemos el siguiente gráfico.

Figura 5.

Aplicando nuestra fórmula, encontramos el volumen de la región.

Este método para calcular el volumen de un sólido de revolución a menudo se denomina método del disco porque la sección transversal es un disco circular de radio R(x).

Rotación sobre el eje y

Incluso cuando el eje de rotación es diferente, las reglas para encontrar el volumen son las mismas, solo necesitamos ajustar la función acorde.

(3)

Ejemplo 3. Encuentra el volumen del sólido generado al girar la región entre el eje y y la curva xy = 2, 1 ≤ y ≤ 4, alrededor del eje y.

Dado que el problema nos pide que giremos el sólido alrededor del eje y, debemos definir nuestra función con y como una variable independiente, por lo que obtenemos x = 2/y. ahora podemos crear un gráfico para esta función.

Figura 6.

Esta será la región que usaremos, y los límites de integración se especificaron en la declaración. Poniendo todo junto obtenemos.

El método de arandela

Una arandela es una placa delgada (típicamente en forma de disco, pero a veces cuadrada) con un agujero (típicamente en el medio), por lo tanto, si la región que agitamos para generar un sólido no bordea o cruza el eje, crea un agujero en el sólido. La sección transversal perpendicular al eje de revolución serán arandelas en lugar de discos. Las dimensiones de una arandela están determinadas por un radio interior r(x) y un radio exterior R(x). ya que es una revolución su área está determinada por una fórmula similar a la del disco.

A= π (radio exterior² – radio interior²) = π[R(x)]² – π[r(x)]² = π(R² – r²)

En consecuencia, su volumen es.

(4)

Ejemplo 4. La región delimitada por la curva y = x² + 1 y la línea y = – x +3 se gira alrededor del eje x para generar un sólido. Encuentre el volumen del sólido.

Nos dan dos funciones y nos piden encontrar el volumen del sólido que se produce al girar la función sobre el eje x. Para estos casos, es una buena idea empezar dibujando las funciones para averiguar cómo se verá el sólido. Además, para ver cuál será el radio interior y exterior y los límites de las integraciones.

Encontramos los límites de integración al encontrar las coordenadas x de los puntos de intersección de la curva y la línea en el gráfico, matemáticamente al igualar ambas funciones entre sí.

Ahora que tenemos toda la información que necesitamos, todo lo que queda es calcular el volumen. 

En la próxima publicación tratará de más ejemplos de secciones transversales.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

• Facebook: https://www.facebook.com/AprendeMatematicasJMD
• Twitter: @JMDciencias
• Correo: institutodecienciasjmd@hotmail.com

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

• Facebook: https://www.facebook.com/JMDFisica
• Blogger: jmdfisica.blogspot.com

Integrales parte 2

Límites De Sumas Finitas

    Las aproximaciones de suma finita que consideramos se volvieron más precisas a medida que aumentaba el número de términos y se reducían los anchos de los subintervalos, pero ¿qué sucede si consideramos un caso en el que el número de casos crece hasta el infinito y el valor del ancho se reduce a cero? En casos como este, donde los números que estamos considerando son infinitesimalmente pequeños o grandes, usamos los límites.

    Tomando nuestro ejemplo de la semana pasada, podemos encontrar el valor límite de las aproximaciones de suma inferior al área de la región debajo del gráfico y arriba del intervalo [0, 1] en el eje x usando rectángulos de igual ancho cuyos anchos se acerquen a cero y cuyo número se acerca al infinito.

    Podemos calcular una aproximación de suma menor usando n rectángulos de igual ancho ∆x = (1 – 0)/n y vemos lo que sucede cuando n à ∞ Comenzamos subdividiendo [0, 1] en n subintervalos de igual ancho

    Cada subintervalo tiene un ancho de 1/n. La función y = 1 – x² es decreciente en [0, 1], y su valor más pequeño en un subintervalo ocurre en el extremo derecho del subintervalo. Entonces, se construye una suma menor con rectángulos cuya altura sobre el subintervalo  es f(k/n) = 1 - (k/n)² dando la suma

    Reescribiendo en notación sigma

    Ahora podemos simplificar este problema aplicando algunas de las propiedades de las sumas finitas

    Aplicamos la regla de la resta y como 1/n es solo una constante, aplicamos las propiedades de valor y múltiplo constantes. Ahora, la suma restante es simplemente una suma de los primeros n cuadrados, que es una suma especial que se está reescribiendo, así como la suma de los primeros n cubos.

Los primeros n cuadrados

Los primeros n cubos

    Y si desean ver la derivación de esta fórmula, puedo crear una publicación adicional esta semana, pero deben informarme en sus comentarios. Mientras tanto, continuemos con nuestro ejercicio.

    Ahora tenemos una expresión para la suma inferior que vale para cualquier n. todo lo que nos queda por hacer es evaluar el límite como n à ∞ y ver si la suma converge.

    Aplicando algunas propiedades de los límites lo dividimos en secciones para un mejor análisis.

    El límite como n à ∞ de 1/n es cero. Entonces, estos términos se cancelan.

    Las aproximaciones de suma inferior convergen a 2/3. Un cálculo similar muestra que las aproximaciones de la suma superior también convergen a 2/3. Cualquier aproximación de suma finita también converge al mismo valor 2/3.

Sumas De Riemann

    La teoría de los límites de las aproximaciones finitas fue precisada por el matemático alemán Bernhard Riemann utilizando lo que hoy se conoce como sumas de Riemann. esta teoría que subyace a la integral definida permite subdividir cualquier función arbitraria sobre un intervalo cerrado que puede tener valores positivos y negativos en subintervalos, no necesariamente de igual amplitud y formar sumas de la misma forma que para las aproximaciones finitas.

    Comenzamos con una función acotada arbitraria ƒ definida en un intervalo cerrado [a, b]. Subdividimos el intervalo [a, b] en subintervalos, no necesariamente de igual ancho y formamos sumas de la misma forma que para las aproximaciones finitas, para ello elegimos n -1 puntos {x₁, x₂, x₃, …, x_n-1} que satisface

a < x₁ < x₂ < x₃ < … < x_n-1 < b

    Si desea que la notación sea consistente, puede denotar a por x₀ y b por x_n.

a = x₀ < x₁ < x₂ < x₃ < … < x_n-1 < x_n = b

 

el conjunto

P = {x₀, x₁, x₂, x₃, …, x_n-1, x_n}

    Se llama partición. La partición divide la región [a, b] en n subintervalos. En cada subintervalo seleccionamos algún punto. El punto elegido en el subintervalo k-ésimo se llama c_k. Luego, en cada subintervalo, colocamos un rectángulo vertical que se extiende desde el eje x para tocar la curva en (c_k, f(c_k)). En cada subintervalo formamos el producto f(c_k)∆x_k y finalmente sumamos todos estos productos.

    Esta suma se llama suma de Riemann. La idea es que no importa cómo elijamos las particiones o los puntos c_k mientras las normas se acerquen a cero. Todas las opciones dan exactamente el mismo límite. Personalmente prefiero trabajar con particiones de igual ancho para simplificar mis cálculos, pero esto es una elección arbitraria, les recomiendo que si quieren mejorar practiquen estos ejemplos usando particiones de diferentes anchuras.

La Integral Definida

    Sea f(x) una función definida en un intervalo cerrado [a, b]. decimos que J es la integral definida de f sobre [a, b] y que J es el límite de las sumas de Riemann si se cumple la siguiente condición:

    Para cualquier número ϵ > 0 existe un número correspondiente δ > 0 tal que para cada partición P = {x₀, x₁, …, x_n} de [a, b] con norma ||P|| < δ y cualquier elección de c_k en [x_k-1, x_k] tenemos 

    Esta definición es muy técnica en lenguaje, pero básicamente lo que implica es un proceso limitante en el que la norma de la partición va a cero. El ancho está determinado por la diferencia entre los dos extremos, por lo que en el caso del primer subintervalo ∆x₁ = x₁ - x₀, y el ancho del segundo se denota por ∆x₂=x₂ - x₁, y así sucesivamente, pero en los casos en que todos los subintervalos tienen el mismo ancho, tenemos ∆x = (b – a)/n y la suma de Riemann se convierte en

    Si el límite cuando n à ∞ existe y es igual a J, entonces J es la integral definida de f en el intervalo [a, b].

    En el límite, el símbolo de la suma se reemplaza por el símbolo de la integral. Esta notación fue introducida por Leibniz. Los valores de la función f(c_k) se reemplazan por una selección continua de valores de la función f(x) y el ancho del subintervalo se convierte en el diferencial dx (recuerde que los pequeños cambios en el límite se representan como derivadas)

    En nuestro ejemplo estamos evaluando la función 1 – x² en el intervalo [0, 1]. Podemos representarlo usando la notación integral como esta.

    Su evaluación se hace usando las antiderivadas. Debemos encontrar la antiderivada de la función y luego evaluar en la diferencia de los puntos finales del intervalo. Para este caso las antiderivadas son fácil de encontrar.

    En el caso del límite de la suma de Riemann, lo representamos como

    Donde debemos elegir una partición para el intervalo si queremos resolverlo. Puedo elegir una partición de igual ancho para todos y usar la ecuación ∆x = (b – a)/n donde a y b son los extremos así que obtengo.

    Entonces mi partición será

    Ahora elijo un punto c_k basada en el ancho que es 1/n en cada sección.  Así que tengo c_k = k/n  

    Con manipulación algebraica tenemos la siguiente expresión 

    Esto es exactamente lo mismo que obtuvimos cuando calculamos el límite de sumas finitas, por lo que su resultado será también el mismo. Indicando que este es el valor real del área.

    Al definir   como un límite de sumas   , nos movimos de izquierda a derecha a lo largo del intervalo [a, b]. pero si nos movemos de derecha a izquierda haciendo las mismas elecciones para cada punto, obtendremos el mismo resultado con un cambio de signo. por lo tanto, podemos concluir.

Orden de integración

    Solo definimos la integral sobre un intervalo [a, b] cuando a < b, pero en el caso cuando a = b ese es el intervalo tiene ancho cero. Esto da ∆x = 0.

Intervalo de ancho cero

    Tenemos otras propiedades que pueden ser útiles al evaluar funciones complicadas.

Múltiplo constante

Cualquier constante k

Suma y Resta

Aditividad

Desigualdad Max-Min

    Si f tiene el valor máximo max f y el valor mínimo min f en [a. b], entonces

Dominación

    Ejemplo. Calcule   y encuentre el área debajo de y = x sobre el intervalo [0, b], b > 0.

    Si hacemos una gráfica de esta función, vemos que el área sombreada es un triángulo. Entonces, usando nuestras técnicas podemos calcular esta área de dos maneras con el límite de las sumas de Riemann y con la integral definida.

    Usando el límite de las sumas de Riemann, debemos calcular para particiones cuya norma tiende a cero. Dado que no importa cómo elijamos nuestra partición, elegiré subintervalos de igual ancho por simplicidad.

    Elegí c_k como el punto final derecho en cada intervalo y mi partición ahora se ve así.

    Ahora podemos aplicar las propiedades que aprendimos de nuestra publicación anterior.

    Tomando el límite cuando n à ∞ obtenemos 

    Este mismo resultado lo obtenemos si aplicamos el signo integral y sus técnicas.

    Me disculpo por toda la teoría y el lenguaje técnico. Hice todo lo posible para simplificarlo lo más posible y hacerlo aceptable para los lectores. Básicamente, si desea poder usar el método de suma de Riemann, siga mis pasos en los ejemplos con cualquier función y luego intente usar el método integral y compare. Este tema me parece muy importante porque muestra cómo surgió la idea de la integración. Es importante aprenderlo en caso de que nos quedemos atascados con una antiderivada (ya que sinceramente no encuentro otro método que la memorización para aprenderlo) porque la suma de Riemann te permite trabajar cualquier función y llegar a su antiderivada básicamente.

    Cualquier sugerencia por favor déjala en los comentarios, y si te gustó compártela con otras personas para que también puedan aprender de ella. En nuestra próxima publicación, hablaremos sobre el Teorema fundamental del cálculo y, con suerte, le agregaré algunos ejemplos.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

• Facebook: https://www.facebook.com/AprendeMatematicasJMD
• Twitter: @JMDciencias
• Correo: institutodecienciasjmd@hotmail.com

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

• Facebook: https://www.facebook.com/JMDFisica
• Blogger: jmdfisica.blogspot.com