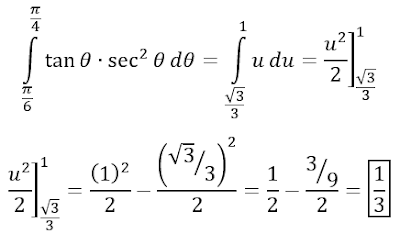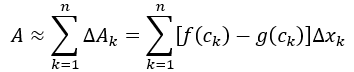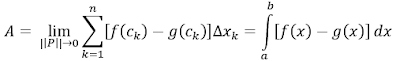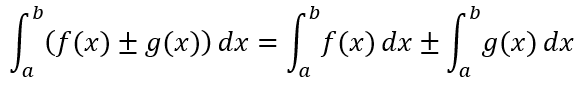Límites
De Sumas Finitas
Las aproximaciones de suma finita que
consideramos se volvieron más precisas a medida que aumentaba el número de
términos y se reducían los anchos de los subintervalos, pero ¿qué sucede si
consideramos un caso en el que el número de casos crece hasta el infinito y el
valor del ancho se reduce a cero? En casos como este, donde los números que
estamos considerando son infinitesimalmente pequeños o grandes, usamos los
límites.
Tomando nuestro ejemplo de la semana
pasada, podemos encontrar el valor límite de las aproximaciones de suma
inferior al área de la región debajo del gráfico y arriba del intervalo [0,
1] en el eje x usando rectángulos de igual ancho cuyos anchos se
acerquen a cero y cuyo número se acerca al infinito.
Podemos
calcular una aproximación de suma menor usando n rectángulos de igual ancho ∆x
= (1 – 0)/n y vemos lo que sucede cuando n à ∞ Comenzamos subdividiendo [0, 1] en
n subintervalos de igual ancho
Cada subintervalo tiene un ancho de 1/n. La función y = 1 – x2
es decreciente en [0, 1], y su valor más pequeño en un subintervalo
ocurre en el extremo derecho del subintervalo. Entonces, se construye una suma
menor con rectángulos cuya altura sobre el subintervalo ![\left[ {\frac{{k - 1}}{n},\frac{k}{n}} \right]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_t_v9yqMCAqdRmckrh-c7Z-ihE5zvU1HogS7ovWkXg4nWWzOPYEaViEwhnctyFAvCRnQ3Mrqx4fMAfExXA52hEDOFEFaO1iYgoWGlrZ05Tp67k6aaMA2NpswV1a5O3lJGp-fayh00CtHW5UR7w4mLIZXUoSYdIb4f8xwbuGmI7zJXhGocGgi0ypmyDhnarBh0QiFm8nSRxZyrjB2IhBCdi15trF1sP1MObQ5-A0B0dVSTEEYz6QhX6hHTLxLFFStKOgPy3taXy0qcMP=s0-d)
es f(k/n) = 1 - (k/n)2 dando la suma Reescribiendo en
notación sigma
Ahora podemos simplificar este
problema aplicando algunas de las propiedades de las sumas finitas
Aplicamos la
regla de la resta y como 1/n es solo una constante, aplicamos las
propiedades de valor y múltiplo constantes. Ahora, la suma restante es
simplemente una suma de los primeros n cuadrados, que es una suma
especial que se está reescribiendo, así como la suma de los primeros n
cubos.
Los
primeros n cuadrados
Los
primeros n cubos
Y
si desean ver la derivación de esta fórmula, puedo crear una publicación
adicional esta semana, pero deben informarme en sus comentarios. Mientras
tanto, continuemos con nuestro ejercicio.
Ahora
tenemos una expresión para la suma inferior que vale para cualquier n.
todo lo que nos queda por hacer es evaluar el límite como n à ∞ y ver si la suma converge.
Aplicando algunas
propiedades de los límites lo dividimos en secciones para un mejor análisis.
El límite como n à ∞ de 1/n es cero. Entonces,
estos términos se cancelan.
Las aproximaciones de suma inferior
convergen a 2/3. Un cálculo similar muestra que las aproximaciones de la
suma superior también convergen a 2/3. Cualquier aproximación de suma
finita también converge al mismo valor 2/3.
Sumas De Riemann
La teoría de los límites de las
aproximaciones finitas fue precisada por el matemático alemán Bernhard Riemann
utilizando lo que hoy se conoce como sumas de Riemann. esta teoría que
subyace a la integral definida permite subdividir cualquier función arbitraria
sobre un intervalo cerrado que puede tener valores positivos y negativos en
subintervalos, no necesariamente de igual amplitud y formar sumas de la misma
forma que para las aproximaciones finitas.
Comenzamos con una función acotada
arbitraria ƒ definida en un intervalo cerrado [a, b].
Subdividimos el intervalo [a, b] en subintervalos, no necesariamente de
igual ancho y formamos sumas de la misma forma que para las aproximaciones
finitas, para ello elegimos n -1 puntos {x1, x2,
x3, …, xn-1} que satisface
a < x1 < x2
< x3 < … < xn-1 < b
Si desea que la notación sea consistente,
puede denotar a por x0 y b por xn.
a = x0 < x1 < x2
< x3 < … < xn-1 < xn = b
el conjunto
P = {x0, x1, x2, x3,
…, xn-1, xn}
Se llama partición. La partición divide
la región [a, b] en n subintervalos. En cada subintervalo seleccionamos algún
punto. El punto elegido en el subintervalo k-ésimo se llama ck.
Luego, en cada subintervalo, colocamos un rectángulo vertical que se extiende
desde el eje x para tocar la curva en (ck, f(ck)).
En cada subintervalo formamos el producto f(ck)∆xk
y finalmente sumamos todos estos productos.
Esta suma se llama suma de Riemann. La
idea es que no importa cómo elijamos las particiones o los puntos ck
mientras las normas se acerquen a cero. Todas las opciones dan exactamente el
mismo límite. Personalmente prefiero trabajar con particiones de igual ancho
para simplificar mis cálculos, pero esto es una elección arbitraria, les
recomiendo que si quieren mejorar practiquen estos ejemplos usando particiones
de diferentes anchuras.
La Integral
Definida
Sea f(x)
una función definida en un intervalo cerrado [a, b]. decimos que J
es la integral definida de f sobre [a, b] y que J es el
límite de las sumas de Riemann si se cumple la siguiente condición:
Para
cualquier número ϵ > 0 existe un número correspondiente δ > 0 tal que para cada partición P = {x0, x1,
…, xn} de [a, b] con norma ||P|| < δ y cualquier elección de ck en [xk-1,
xk] tenemos
Esta definición
es muy técnica en lenguaje, pero básicamente lo que implica es un proceso
limitante en el que la norma de la partición va a cero. El ancho está
determinado por la diferencia entre los dos extremos, por lo que en el caso del
primer subintervalo ∆x1 = x1 - x0, y el
ancho del segundo se denota por ∆x2=x2 - x1,
y así sucesivamente, pero en los casos en que todos los subintervalos tienen el
mismo ancho, tenemos ∆x = (b – a)/n y la suma de Riemann se convierte en
Si el límite
cuando n à ∞ existe y es igual a J,
entonces J es la integral definida de f en el intervalo [a, b].
En el límite, el
símbolo de la suma se reemplaza por el símbolo de la integral. Esta notación
fue introducida por Leibniz. Los valores de la función f(ck)
se reemplazan por una selección continua de valores de la función f(x) y
el ancho del subintervalo se convierte en el diferencial dx (recuerde
que los pequeños cambios en el límite se representan como derivadas)
En nuestro
ejemplo estamos evaluando la función 1 – x2 en el intervalo [0,
1]. Podemos representarlo usando la notación
integral como esta.
Su evaluación
se hace usando las antiderivadas. Debemos encontrar la antiderivada de la
función y luego evaluar en la diferencia de los puntos finales del intervalo.
Para este caso las antiderivadas son fácil de encontrar.
En el caso del límite de la suma de Riemann,
lo representamos como
Donde debemos elegir una partición
para el intervalo si queremos resolverlo. Puedo elegir una partición de igual
ancho para todos y usar la ecuación ∆x = (b – a)/n donde a y b
son los extremos así que obtengo.
Entonces mi partición será
Ahora elijo un punto ck
basada en el ancho que es 1/n en cada sección.
Así que tengo ck = k/n
Con manipulación algebraica tenemos la
siguiente expresión
Esto es
exactamente lo mismo que obtuvimos cuando calculamos el límite de sumas
finitas, por lo que su resultado será también el mismo. Indicando que este es
el valor real del área.
Al definir
como un límite de sumas
, nos movimos de izquierda
a derecha a lo largo del intervalo [a, b]. pero si nos movemos de
derecha a izquierda haciendo las mismas elecciones para cada punto, obtendremos
el mismo resultado con un cambio de signo. por lo tanto, podemos concluir.
Orden de integración
Solo definimos la
integral sobre un intervalo [a, b] cuando a < b, pero en el
caso cuando a = b ese es el intervalo tiene ancho cero. Esto da ∆x =
0.
Intervalo de ancho cero
Tenemos otras propiedades que pueden
ser útiles al evaluar funciones complicadas.
Múltiplo constante
Cualquier constante k
Suma y Resta
Aditividad
Desigualdad Max-Min
Si f tiene el valor máximo max
f y el valor mínimo min f en [a. b], entonces
Dominación
Ejemplo. Calcule
y encuentre el área debajo
de y = x sobre el intervalo [0, b], b > 0.
Si hacemos una
gráfica de esta función, vemos que el área sombreada es un triángulo. Entonces,
usando nuestras técnicas podemos calcular esta área de dos maneras con el
límite de las sumas de Riemann y con la integral definida.
Usando el límite
de las sumas de Riemann, debemos calcular para particiones cuya norma tiende a
cero. Dado que no importa cómo elijamos nuestra partición, elegiré
subintervalos de igual ancho por simplicidad.
Elegí ck
como el punto final derecho en cada intervalo y mi partición ahora se ve así.
Ahora podemos aplicar las propiedades
que aprendimos de nuestra publicación anterior.
Tomando el límite cuando n à ∞ obtenemos
Este mismo resultado lo obtenemos si
aplicamos el signo integral y sus técnicas.
Me disculpo por
toda la teoría y el lenguaje técnico. Hice todo lo posible para simplificarlo
lo más posible y hacerlo aceptable para los lectores. Básicamente, si desea
poder usar el método de suma de Riemann, siga mis pasos en los ejemplos con
cualquier función y luego intente usar el método integral y compare. Este tema
me parece muy importante porque muestra cómo surgió la idea de la integración.
Es importante aprenderlo en caso de que nos quedemos atascados con una
antiderivada (ya que sinceramente no encuentro otro método que la memorización
para aprenderlo) porque la suma de Riemann te permite trabajar cualquier
función y llegar a su antiderivada básicamente.
Cualquier
sugerencia por favor déjala en los comentarios, y si te gustó compártela con
otras personas para que también puedan aprender de ella. En nuestra próxima
publicación, hablaremos sobre el Teorema fundamental del cálculo y, con suerte,
le agregaré algunos ejemplos.
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
También pueden seguir nuestro otro blog si les
interesa aprender sobre el interesante mundo de la física.
![u = \sqrt[3]{{{z^2} + 1}}](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_uUPAx7GAuHvhqv4imT1fV4Ri4yfwn3FSqkg4Zl26Q48E8i_8PuWr2fez0HIsxOiAzkehuOGuYZ6zJLYTI-LuLdSWWg31muEufU0SOi6jevhtDegR1HCrC9MAtGoMj3OHSun9PF_LAjb8T-ZqLlfxEwmpbL0170LWaVDWxE7lcaQOPKlDN-L5ubc4hHkRMGpJGaEvRucZY27_6lRPC7OGqDfjoQtt0OIb5n=s0-d)
à u3
= z2 +1; 3u2 du = 2z
.
