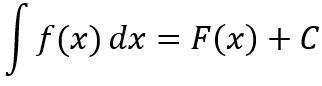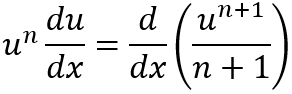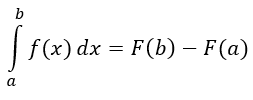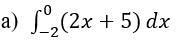Hasta ahora, hemos estudiado funciones sobre un intervalo finito [a, b] que nos permite encontrar una integral definida en el intervalo especificado. La solución es particular y específica de esa función y ese intervalo (si cambiamos el intervalo, cambiamos la solución). La integral indefinida de una función es el conjunto de todas las antiderivadas. Como dos antiderivadas cualesquiera difieren en una constante, la integral indefinida se representa como
Donde C es cualquier constante arbitraria.
Mientras que la solución de una integral definida es un número, una integral indefinida nos da una función más una constante arbitraria.
Ejemplo:
Estas funciones son muy sencillas y sus antiderivadas son simples, pero la mayoría de las funciones no son así, por lo que debemos desarrollar técnicas más generales para encontrar antiderivadas. Un método que ya probamos fue el método de sustitución, así que ampliémoslo aquí.
Ejecutar la regla de la cadena al revés
Si u es una función diferenciable de x y n es cualquier número diferente de -1, la regla de la cadena nos dice que
Esta misma ecuación dice queEsta idea de cambiar o sustituir una expresión compleja por una nueva variable que simplifica la función es la clave del método de sustitución.
Ejemplo 2. Resuelve la integral.
Hacemos u =
x3 + x entonces
à (3x2 + 1) dx. Con esto podemos sustituir la expresión.
Para que la sustitución se realice correctamente, las expresiones deben coincidir con precisión.
- Sustituye u = g(x) y
. Reescribir la integral
.
- Integrar con respecto a u.
- Reemplace u por g(x) en el resultado.
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden seguir nuestro otro blog si les
interesa aprender sobre el interesante mundo de la física.
- Facebook: https://www.facebook.com/JMDFisica
- Blogger: jmdfisica.blogspot.com