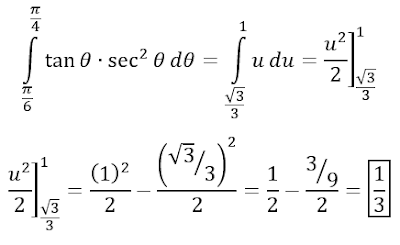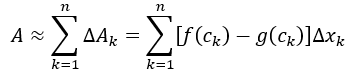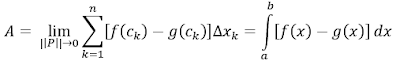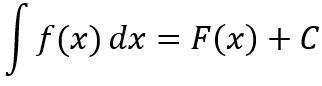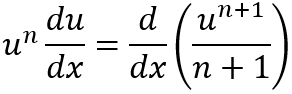Aprende Matemáticas JMD

Sigamos con otro ejemplo.

Quiero intentar encontrar el límite de esta expresión usando dos sustituciones diferentes. La primera sustitución será u = z² + 1 à du = 2z dz, así que reescribamos y evaluemos nuestra integral.

Ahora quiero intentar una sustitución diferente; $u = \sqrt[3]{{{z^2} + 1}}$ à u³ = z² +1; 3u² du = 2z

Obtuvimos la misma respuesta que era de esperar porque esta es la solución más general.

Volviendo a las integrales definidas, existen dos métodos para evaluar una integral definida por sustitución. Un método es encontrar una antiderivada usando sustitución y luego evaluar la integral definida aplicando el Teorema de Evaluación. Hemos usado este método constantemente ya que es muy simple, el otro método extiende el proceso de sustitución directamente a integrales definidas al cambiar los límites de integración.

Teorema: Si g’ es continua en el intervalo [a, b] y f es continua en el rango de g(x) = u, entonces

Para usar la fórmula, haga la sustitución u = g(x) y du = g’(x) dx que usaría para evaluar la integral indefinida correspondiente. Luego evalúa la sustitución en los puntos x = a y x = b para obtener los nuevos puntos g(a) y g(b).

Ejemplo 1. Evaluar $\int\limits_{ - 1}^1 {3{x^2}\sqrt {{x^3} + 1} \,dx}$ .

Sea u = x³ +1, du = 3x² dx

Cuando x = -1, u = (-1)³ + 1 = 0

Cuando x = 1, u = (1)³ +1 = 2

Así que los nuevos límites de la integral son.

¿Qué método es mejor? En general, es mejor conocer ambos métodos y usar el que parezca mejor en ese momento, ya que cada integral es diferente y puede requerir diferentes enfoques.

Ejemplo 2 Evaluar $\int\limits_{\pi /6}^{\pi /4} {\tan \theta \cdot {{\sec }^2}\theta \,d\theta }$

Sea u = tan θ, du = sec² θ dθ

Cuando θ = π/4, u = tan(π/4) = 1

Cuando θ = π/6, u = tan(π/6) = √3/3

Este teorema tiene otra implicación importante. Simplifica el cálculo de integrales definidas de funciones pares e impares en un intervalo simétrico [-a, a]. Un intervalo simétrico es fácil de detectar debido a la distribución de puntos.

Sea f continua en el intervalo simétrico [-a, a]

Si f es par, entonces $\int\limits_{ - a}^a {f(x)\,dx = 2\int\limits_0^a {f(x)dx} }$ .

Si f es impar, entonces $\int\limits_{ - a}^a {f(x)\,dx = 0}$

Puedes practicar para encontrar la prueba de esta afirmación usando la sustitución u y dividiendo la integral en dos regiones: a ≤ x ≤ 0 y 0 ≤ x ≤ a.

Evaluar $\int\limits_{ - 2}^2 {({x^4} - 4{x^2} + 6)dx}$

Podemos evaluar la integral tal como es, o podemos confirmar para ver si la función es par o impar. Para eso sustituimos la variable de la función por su negativo x à -x y si obtenemos a cambio la función original la función es par, si obtenemos la función con sus signos cambiados la función es impar. Para este caso:

f(x) = x⁴ – 4x² + 6 à f(-x) = (-x)⁴ – 4(-x)² + 6 = x⁴ – 4x² + 6

Podemos decir f(-x) = f(x) por lo tanto la función es par

Puedes confirmar este resultado simplemente tomando la integral sin reducir los límites del intervalo.

Área entre curvas

Supongamos que queremos encontrar el área de una región que está limitada por arriba por la curva y₁ = f(x), por abajo por la curva y₂ = g(x), y por la izquierda y la derecha por las líneas x = a y x = b. La región puede tener accidentalmente una forma cuya área podamos encontrar con geometría como en la figura A, pero si ƒ y g son funciones continuas arbitrarias, por lo general tenemos que encontrar el área con una integral como en la figura B.

El área delimitada por estas dos funciones viene dada por la diferencia entre la curva superior y la curva inferior

y₁ – y₂ = f (x) – g (x)

Para ver cuál debería ser la integral, usamos la misma técnica que usamos cuando definimos la integral. primero aproximamos la región con n rectángulos verticales basados en una partición P = {x₀, x₁, …, x_n} de [a,b]. el área del k-ésimo rectángulo es.

∆A_k = Altura × ancho = [f (c_k ) – g(c_k )]∆x_k

_{Al sumar áreas de los n rectángulos, creamos nuestra suma de Riemann para aproximar el área.}

Como ||P|| à 0 las sumas se acercan al límite, dando así el área de la región para ser el valor de la integral.

Si f y g son continuas con f(x) ≥ g(x) a lo largo de [a, b], entonces el área de la región entre las curvas es la integral de (f – g) de a a b.

Al aplicar esta definición, es útil graficar las curvas. El gráfico revela qué curva es la curva superior ƒ y cuál es la curva inferior g. También te ayuda a encontrar los límites de integración si no se dan. Es posible que deba encontrar dónde se cruzan las curvas para determinar los límites de integración, y esto puede implicar resolver la ecuación f(x) = g(x).

Ejemplos 3.

Encuentre el área de la región limitada arriba por la curva y = 2e^-x + x, abajo por la curva y = e^x/2, a la izquierda por x = 0 y a la derecha por x = 1.

En este primer ejemplo no necesitamos la gráfica ya que se nos ha dado toda la información esencial, por lo tanto podemos proceder a evaluar la integral.

El valor de esta área corresponde a la siguiente figura.

Encuentra el área de la región encerrada por la parábola y = 2 – x² y la recta y = -x

En este caso no nos dan los límites de integración y no sabemos qué función corresponde al límite superior o inferior, por lo que primero debemos dibujar las dos curvas e igualar las dos funciones para encontrar los límites de integración. .

El área sombreada nos dice que el límite superior es la función y = 2 – x² y el límite inferior en la función y = – x. También muestra que los puntos de intersección de las funciones ocurren en x = -1 y x = 2, estos podrían ser los límites de integración, así que confirmemos resolviendo la ecuación.

Como era de esperar por lo que pudimos analizar del gráfico. Ahora tenemos todo lo que necesitamos para resolver nuestra integral.

Si la fórmula de una curva delimitada cambia en uno o más puntos, subdividimos la región en subregiones que correspondan a los cambios de fórmula y aplicamos la fórmula del área entre curvas a cada subregión. Trabajemos un ejemplo un poco más complicado esta vez para ver esta propiedad.

Encuentre el área en el primer cuadrante que está delimitada por la función y = √x y y = x – 2.

Primero, dibujamos el gráfico.

Como solo nos interesa el primer cuadrante de la gráfica, esto muestra que el límite superior de la región es la gráfica de y = √x. el límite inferior, por otro lado, cambia de g(x) = 0 para 0 ≤ x ≤ 2 a g(x) = 2 – x para 2 ≤ x ≤ 4. Así que subdividimos la región en x = 2 en la subregión A y B.

Los límites de integración para la región A son a = 0 y b = 2. El límite izquierdo para la región B es a = 2. Para encontrar el límite derecho, igualamos las funciones entre sí.

El valor x = 1 es una raíz fuera del límite de la función, por lo que solo el valor x = 4 satisface la ecuación. El límite de la derecha es b = 4.

Puede apreciar que se tomaron muchos pasos para resolver este problema.

Integración con respecto a y

Si las curvas delimitadoras de una región se describen mediante funciones de y, los rectángulos de aproximación son horizontales en lugar de verticales y la fórmula básica tiene y en lugar de x. la formula de la integral cambia sus variables.

En esta ecuación, f siempre denota la curva de la derecha y g la curva de la izquierda, por lo que f(y) – g(y) no es negativa. Vamos a calcular la integral de nuestro ultimo ejemplo, para ello debemos modificar la ecuacion haciendo y la variable dependiente.

y = √x à x = y²; y = x – 2 à x = y + 2

Como las variables en este caso han sido invertidas, límite de la derecha x = y + 2 mientras que el límite de la izquierda es x = y²; el límite inferior de integración es c = 0 mientras que el límite superior debemos encontrarlo.

El límite superior es d = 2 ya que -1 esta fuera del intervalo permitido. Ahora si podemos construir nuestra integral y resolverlo.

Como podemos ver obtenemos el mismo valor para el área ya que estamos trabajando el mismo problema, pero fue mucho mas fácil, es decir que hay casos donde la integración de una variable es más simple que la otra. Esto es muy importante a recordar pues será útil en integraciones de múltiples dimensiones más adelante.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

Facebook: https://www.facebook.com/AprendeMatematicasJMD
Twitter: @JMDciencias
Correo: institutodecienciasjmd@hotmail.com

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física.

Facebook: https://www.facebook.com/JMDFisica
Blogger: jmdfisica.blogspot.com

Hasta ahora, hemos estudiado funciones sobre un intervalo finito [a, b] que nos permite encontrar una integral definida en el intervalo especificado. La solución es particular y específica de esa función y ese intervalo (si cambiamos el intervalo, cambiamos la solución). La integral indefinida de una función es el conjunto de todas las antiderivadas. Como dos antiderivadas cualesquiera difieren en una constante, la integral indefinida se representa como

Donde C es cualquier constante arbitraria.

Mientras que la solución de una integral definida es un número, una integral indefinida nos da una función más una constante arbitraria.

Ejemplo:

Estas funciones son muy sencillas y sus antiderivadas son simples, pero la mayoría de las funciones no son así, por lo que debemos desarrollar técnicas más generales para encontrar antiderivadas. Un método que ya probamos fue el método de sustitución, así que ampliémoslo aquí.

Ejecutar la regla de la cadena al revés

Si u es una función diferenciable de x y n es cualquier número diferente de -1, la regla de la cadena nos dice que

Esta misma ecuación dice que $\frac{{{u^{n + 1}}}}{{n + 1}}$ es una de las antiderivadas de la función ${u^n}\frac{{du}}{{dx}}$ asi que

Que se puede simplificar por du = du/dx.

Esta idea de cambiar o sustituir una expresión compleja por una nueva variable que simplifica la función es la clave del método de sustitución.

Ejemplo 2. Resuelve la integral.

Para resolver esta integración, podemos expandir la exponencial y multiplicar y obtener una expresión en la que podamos usar las propiedades de la integración, pero esta tarea puede llevar mucho tiempo, por lo que lo que podemos hacer es encontrar una sustitución que se ajuste a nuestro modelo anterior.

Hacemos u = x³ + x entonces $du = \,\frac{{du}}{{dx}}dx$ à (3x² + 1) dx. Con esto podemos sustituir la expresión.

Para que la sustitución se realice correctamente, las expresiones deben coincidir con precisión.

Sea u = 2x + 3 à du = 2dx pero la expresión du no coincide con la expresión dx por lo que debemos manipular los términos para que coincida. ½ du = dx.

Teorema: si u = g(x) es una función derivable cuyo recorrido es un intervalo I, y f es continua en I, entonces.

La regla de sustitución proporciona 3 pasos para que el método de sustitución evalúe la integral.

Donde f y g’ son funciones continuas:

Sustituye u = g(x) y $du = \frac{{du}}{{dx}}dx = \frac{{dg}}{{dx}}dx = g'(x)dx$ . Reescribir la integral $\int {f(u)du}$ .
Integrar con respecto a u.
Reemplace u por g(x) en el resultado.

Un integrando puede requerir alguna manipulación algebraica antes de que se pueda aplicar la sustitución. Si la sustitución no simplifica la función, podemos aplicarla de nuevo, o hemos hecho una elección incorrecta. El punto es que la expresión sustituida debe ser más simple que la expresión original, no más complicada.

Ejemplo 3:

Esta expresión es similar a la última integral que resolvimos, excepto que esta vez tenemos un término adicional, por lo que podemos aplicar la misma sustitución y manipularla algebraicamente para encontrar una expresión para x en términos de u.