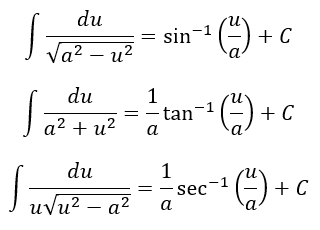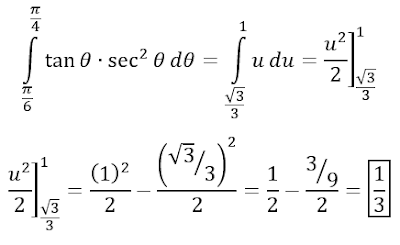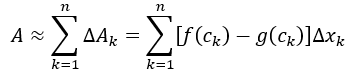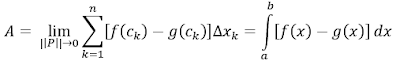lunes, 5 de septiembre de 2022

Función Trigonométrica Inversa

    Las funciones trigonométricas relacionan un ángulo de un triángulo rectángulo con las proporciones de las longitudes de dos lados, al conocer el ángulo podemos calcular la proporción de dos lados cualesquiera de un triángulo rectángulo. Estas funciones son seno, coseno, tangente, cotangente, secante y cosecante. Algunas de estas funciones están escritas en términos de otras funciones y pueden escribirse en forma compleja usando la fórmula de Euler:

    Podemos memorizar las proporciones o calcularlas en base a su compleja definición siempre que los ángulos se escriban en radianes en lugar de grados.

    En matemáticas hasta ahora, hemos visto que cada operación tiene múltiples enfoques y la memorización es un buen atajo pero no una herramienta imprescindible para hacer las operaciones. Otra propiedad importante de las matemáticas es que la mayoría de las operaciones (las que hemos cubierto hasta ahora) son reversibles. Puedes ir y venir y aprender cosas nuevas al respecto. Las operaciones que son reversibles se consideran tener una operación inversa.
    Ya conocemos las operaciones inversas. Por ejemplo, la suma y la resta son operaciones inversas entre sí. La idea es la misma en trigonometría. Las funciones trigonométricas inversas hacen lo contrario de las funciones trigonométricas "normales". En general, si conoce la relación trigonométrica pero no el ángulo, puede usar la función trigonométrica inversa correspondiente para encontrar el ángulo.
¡Alerta de malentendidos!
    La expresión sin-1(x), no es lo mismo que 1/sin(x). En otras palabras, el −1 no es un exponente. En cambio, simplemente significa función inversa. Otra forma de representar las funciones trigonométricas     inversas es con el uso del prefijo arc- que posee la misma connotación que -1 (sin-1 = arcsin).
Dado que ninguna de las seis funciones trigonométricas es uno a uno, deben estar restringidas para tener funciones inversas. Por lo tanto, los rangos de resultados de las funciones inversas son subconjuntos de los dominios de las funciones originales.

Nombres

Notación

Definición

Rango en radianes

arco seno

y = arcsin (x)

x = sin (y)

- π/2 <y < π/2

arco coseno

y = arccos (x)

x = cos(y)

0 < y < π

arco tangente

y = arctan (x)

x = tan(y)

- π/2 < y < π/2

arco cotangente

y = arccot (x)

x = cot(y)

0 < y < π

arco secante

y = arcsec (x)

x = sec(y)

0 < y < π/2 ó π/2 < y < π

arco cosecante

y = arccsc (x)

x = csc(y)

- π/2 < y < 0 ó 0< y < π/2

    Ahora que entendemos qué son las funciones trigonométricas inversas, veamos sus propiedades derivadas e integrales.
  •    Si f(x) y g(x) son funciones inversas entre sí (f(g(x)) = x y g(f(x)) = x), entonces la derivada g'(x) se puede obtener usando la siguiente fórmula.
    En el caso del seno inverso, tenemos.
    Esta no es una fórmula muy útil. Veamos si podemos conseguir una fórmula mejor. Comencemos recordando la definición de la función seno inversa.
    Usando la primera parte de esta definición, el denominador en la derivada se convierte en,
    Ahora podemos aplicar

    Usando la segunda parte de la definición de la función seno inversa, el denominador se convierte en.
    Poniendo todo esto junto, hemos encontrado la derivada para el arco seno.
    Aplicamos el mismo método para encontrar todas las demás derivadas y las compilamos en una tabla.


    Pero, ¿y si la función inversa tiene una función de x en lugar de un valor como u(x)? ¿Cómo afectaría esto a la derivada?
    Lo bueno es que el cambio no es tan grande simplemente tenemos que aplicar la regla de la cadena. Para ver esto, podemos reescribir las fórmulas anteriores en una más general para ver cómo se verán afectadas.
    Sea u = u(x). las derivadas de las funciones trigonométricas inversas con respecto a x son.


    Ahora las derivadas no son solo para valores de x sino para todo tipo de funciones que dependen de x. Ahora que conocemos las derivadas, podemos usarlas para encontrar integrales del mismo tipo.
    Sea a cualquier número distinto de cero y u una función de x.
    Ahora lo más importante es poder reconocer este patrón con otras funciones. Examinemos algunos ejemplos.

Sea u2 = x2 à u = x y du = dx; a2 = 16 à a = 4.

Sea u2 = 4x2 à u = 2x reescribiendo x = u/2 and du = 2dx; a2 = 1 à a = 1.

    ¿Qué pasa con una integral de esta forma?
    Para resolver este problema, utilizamos una técnica llamada integración por partes que aún no hemos explorado. Entonces, por ahora lo mantendremos en espera hasta que expliquemos esta técnica y haremos ejemplos de estas funciones inversas.

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

Publicadas por a la/s No hay comentarios.:
Etiquetas: , , , ,

lunes, 6 de junio de 2022

Mas Ejemplos de Integrales.

     Vamos a trabajar algunos ejercicios para ver las propiedades que aprendimos en la pasada publicación.

Evalúa las integrales.

    Este es un ejercicio bastante directo. Primero debemos hacer una sustitución que permita la simplificación del ejercicio y luego evaluar la sustitución en los límites para obtener nuevos límites. Recordemos que la raíz cuadrada es igual que la potencia ½. Para nuestra sustitución elegí.

  • Sea u = y + 1 à du = dy
  • Cuando y = 0, u = 1
  • Cuando y = 3, u = 4

Nuestra sustitución será. 



    En este caso la sustitución añade un término extra así que debemos ser cuidadoso con eso.

  • Sea u = 1 + t4 à du = 4t3 dt; ¼ du = t3 dt
  • Cuando t = 0, u = 1
  • Cuando t = 1, u = 2

    La sustitución hizo de este problema algo bastante simple. Otro método que podíamos utilizar fue el de la distribución de potencial y luego evaluar la integral para cada termino. La integral a evaluar seria la siguiente.

t3(1 + t4)3 = t3(1 + 3t4 + 3t8 + t12)

= t15 + 3t11 + 3t7 + t3



    For this problem the important fact to remember is that the denominator is simply a negative exponential.

  • Sea u = 4 + r2 à du 2r dr; ½ du = r dr
  • Cuando r = 0, u = 4
  • Cuando r = 1, u = 5





  • Sea u = 1 – cos (3t) à du = 3sin (3t) dt; 1/3 du = sin (3t) dt
  • Cuando t = 0, u = 0
  • Cuando t = π/6, u = 1


Encuentra el área de la región sombreada.

    Los siguientes ejercicios tratan sobre el análisis grafico para determinar las propiedades que necesitamos para calcular áreas usando integrales. Para ello necesitamos conocer la función que compone el área sombreada y los limites tanto del eje x como del eje y ya que no sabemos cual de los dos ejes nos facilitara la integral.


    Tenemos que la función es descrita en términos de x así que evaluaremos esta integral con respecto a x. los límites de integración con respecto a x son – 2 < x < 2 lo que lo hace un intervalo simétrico Antes de tratar de resolver voy a confirmar si la función es par o impar. Ya que los límites de integración satisfacen la condición de simetría. 

    La función es impar por lo que la integral debe ser cero. Esto también lo podemos apreciar al ver la gráfica ya que el área de la función es como un reflejo de si misma. Vamos a confirmarlo.

  • Sea u = 4 – x2 à du = – 2x dx; – ½ du = x dx


    Este caso es bastante directo, tenemos una función definida en términos de x y su intervalo es – π < x < 0. Si hay algo que nos puede servir para solucionar este problema es el conocimiento de que el seno es una función impar y el coseno es una función par, es decir sin (–x) = – sin (x); cos (–x) = cos (x).

  • Sea u = 1+ cos x à du = – sin x dx; – du = sin x dx



    In this case we can rewrite the functions to integrate with respect to x, but it will be easier to Integrate with respect to y instead. El intervalo de las funciones va 0 < y < 1 y como estamos usando el eje y el orden de las funciones va de derecha a izquierda, obtenemos f(y) = 12y2 – 12y3 y g(y) = 2y2 – 2y.


 

    Podemos integrar esta área usando el eje x. de arriba hacia abajo tenemos que f(x) = 1 y g(x) = cos2 x y los límites de integración a = 0 y b = π.


    Para resolver este problema utilizaremos dos identidades trigonométricas para simplificar el problema.


Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

Publicadas por a la/s No hay comentarios.:
Etiquetas: , , , , , , ,

lunes, 23 de mayo de 2022

Límites de integración en el método de Sustitución y área entre curvas

    Sigamos con otro ejemplo.


    Quiero intentar encontrar el límite de esta expresión usando dos sustituciones diferentes. La primera sustitución será u = z2 + 1 à du = 2z dz, así que reescribamos y evaluemos nuestra integral.


    Ahora quiero intentar una sustitución diferente; u = \sqrt[3]{{{z^2} + 1}}  à u3 = z2 +1; 3u2 du = 2z

    Obtuvimos la misma respuesta que era de esperar porque esta es la solución más general.
    Volviendo a las integrales definidas, existen dos métodos para evaluar una integral definida por sustitución. Un método es encontrar una antiderivada usando sustitución y luego evaluar la integral definida aplicando el Teorema de Evaluación. Hemos usado este método constantemente ya que es muy simple, el otro método extiende el proceso de sustitución directamente a integrales definidas al cambiar los límites de integración.
  • Teorema: Si g’ es continua en el intervalo [a, b] y f es continua en el rango de g(x) = u, entonces
    Para usar la fórmula, haga la sustitución u = g(x) y du = g’(x) dx que usaría para evaluar la integral indefinida correspondiente. Luego evalúa la sustitución en los puntos x = a y x = b para obtener los nuevos puntos g(a) y g(b).
Ejemplo 1. Evaluar \int\limits_{ - 1}^1 {3{x^2}\sqrt {{x^3} + 1} \,dx}.

Sea u = x3 +1, du = 3x2 dx

Cuando x = -1, u = (-1)3 + 1 = 0

Cuando x = 1, u = (1)3 +1 = 2

Así que los nuevos límites de la integral son.

    ¿Qué método es mejor? En general, es mejor conocer ambos métodos y usar el que parezca mejor en ese momento, ya que cada integral es diferente y puede requerir diferentes enfoques.

Ejemplo 2 Evaluar \int\limits_{\pi /6}^{\pi /4} {\tan \theta \cdot {{\sec }^2}\theta \,d\theta }

Sea u = tan θ, du = sec2 θ dθ

Cuando θ = π/4, u = tan(π/4) = 1

Cuando θ = π/6, u = tan(π/6) = √3/3

    Este teorema tiene otra implicación importante. Simplifica el cálculo de integrales definidas de funciones pares e impares en un intervalo simétrico [-a, a]. Un intervalo simétrico es fácil de detectar debido a la distribución de puntos.

Sea f continua en el intervalo simétrico [-a, a]

Si f es par, entonces \int\limits_{ - a}^a {f(x)\,dx = 2\int\limits_0^a {f(x)dx} }.

Si f es impar, entonces \int\limits_{ - a}^a {f(x)\,dx = 0}

    Puedes practicar para encontrar la prueba de esta afirmación usando la sustitución u y dividiendo la integral en dos regiones: a ≤ x ≤ 0 y 0 ≤ x ≤ a.

  • Evaluar \int\limits_{ - 2}^2 {({x^4} - 4{x^2} + 6)dx}
    Podemos evaluar la integral tal como es, o podemos confirmar para ver si la función es par o impar. Para eso sustituimos la variable de la función por su negativo x à -x y si obtenemos a cambio la función original la función es par, si obtenemos la función con sus signos cambiados la función es impar. Para este caso:

f(x) = x4 – 4x2 + 6  à f(-x) = (-x)4 – 4(-x)2 + 6 = x4 – 4x2 + 6 

Podemos decir f(-x) = f(x) por lo tanto la función es par

    Puedes confirmar este resultado simplemente tomando la integral sin reducir los límites del intervalo.
Área entre curvas

    Supongamos que queremos encontrar el área de una región que está limitada por arriba por la curva y1 = f(x), por abajo por la curva y2 = g(x), y por la izquierda y la derecha por las líneas x = a y x = b. La región puede tener accidentalmente una forma cuya área podamos encontrar con geometría como en la figura A, pero si ƒ y g son funciones continuas arbitrarias, por lo general tenemos que encontrar el área con una integral como en la figura B.

    El área delimitada por estas dos funciones viene dada por la diferencia entre la curva superior y la curva inferior

y1 – y2 = f (x) – g (x)

    Para ver cuál debería ser la integral, usamos la misma técnica que usamos cuando definimos la integral. primero aproximamos la región con n rectángulos verticales basados en una partición P = {x0, x1, …, xn} de [a,b]. el área del k-ésimo rectángulo es.

∆Ak = Altura × ancho = [f (ck ) – g(ck )]∆xk

    Al sumar áreas de los n rectángulos, creamos nuestra suma de Riemann para aproximar el área.


    Como ||P|| à 0 las sumas se acercan al límite, dando así el área de la región para ser el valor de la integral.
  • Si f y g son continuas con f(x) ≥ g(x) a lo largo de [a, b], entonces el área de la región entre las curvas es la integral de (f – g) de a a b.

    Al aplicar esta definición, es útil graficar las curvas. El gráfico revela qué curva es la curva superior ƒ y cuál es la curva inferior g. También te ayuda a encontrar los límites de integración si no se dan. Es posible que deba encontrar dónde se cruzan las curvas para determinar los límites de integración, y esto puede implicar resolver la ecuación f(x) = g(x).

Ejemplos 3.
  • Encuentre el área de la región limitada arriba por la curva  y = 2e-x + x, abajo por la curva y = ex/2, a la izquierda por x = 0 y a la derecha por x = 1.
    En este primer ejemplo no necesitamos la gráfica ya que se nos ha dado toda la información esencial, por lo tanto podemos proceder a evaluar la integral.
    El valor de esta área corresponde a la siguiente figura.
  • Encuentra el área de la región encerrada por la parábola y = 2 – x2 y la recta y = -x
    En este caso no nos dan los límites de integración y no sabemos qué función corresponde al límite superior o inferior, por lo que primero debemos dibujar las dos curvas e igualar las dos funciones para encontrar los límites de integración. .
    El área sombreada nos dice que el límite superior es la función y = 2 – x2 y el límite inferior en la función y = – x. También muestra que los puntos de intersección de las funciones ocurren en x = -1 y x = 2, estos podrían ser los límites de integración, así que confirmemos resolviendo la ecuación.
    Como era de esperar por lo que pudimos analizar del gráfico. Ahora tenemos todo lo que necesitamos para resolver nuestra integral.
    Si la fórmula de una curva delimitada cambia en uno o más puntos, subdividimos la región en subregiones que correspondan a los cambios de fórmula y aplicamos la fórmula del área entre curvas a cada subregión. Trabajemos un ejemplo un poco más complicado esta vez para ver esta propiedad.
  • Encuentre el área en el primer cuadrante que está delimitada por la función y = √x y y = x – 2.
Primero, dibujamos el gráfico.
    Como solo nos interesa el primer cuadrante de la gráfica, esto muestra que el límite superior de la región es la gráfica de y = √x. el límite inferior, por otro lado, cambia de g(x) = 0 para 0 ≤ x ≤ 2 a g(x) = 2 – x para 2 ≤ x ≤ 4. Así que subdividimos la región en x = 2 en la subregión A y B.
    Los límites de integración para la región A son a = 0 y b = 2. El límite izquierdo para la región B es a = 2. Para encontrar el límite derecho, igualamos las funciones entre sí.
    El valor x = 1 es una raíz fuera del límite de la función, por lo que solo el valor x = 4 satisface la ecuación. El límite de la derecha es b = 4.
    Puede apreciar que se tomaron muchos pasos para resolver este problema.

Integración con respecto a y

    Si las curvas delimitadoras de una región se describen mediante funciones de y, los rectángulos de aproximación son horizontales en lugar de verticales y la fórmula básica tiene y en lugar de x. la formula de la integral cambia sus variables.
    En esta ecuación, f siempre denota la curva de la derecha y g la curva de la izquierda, por lo que f(y) – g(y) no es negativa. Vamos a calcular la integral de nuestro ultimo ejemplo, para ello debemos modificar la ecuacion haciendo y la variable dependiente.

y = √x à x = y2; y = x – 2 à x = y + 2

    Como las variables en este caso han sido invertidas, límite de la derecha x = y + 2 mientras que el límite de la izquierda es x = y2; el límite inferior de integración es c = 0 mientras que el límite superior debemos encontrarlo.

    El límite superior es d = 2 ya que -1 esta fuera del intervalo permitido. Ahora si podemos construir nuestra integral y resolverlo.

    Como podemos ver obtenemos el mismo valor para el área ya que estamos trabajando el mismo problema, pero fue mucho mas fácil, es decir que hay casos donde la integración de una variable es más simple que la otra. Esto es muy importante a recordar pues será útil en integraciones de múltiples dimensiones más adelante. 

Ahora pueden seguirnos y contactarnos a través de Facebook, Twitter y correo electrónico.

 

 

También pueden seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de la física. 

 

Publicadas por a la/s No hay comentarios.:
Etiquetas: , , , , , ,
Suscribirse a: Entradas (Atom)