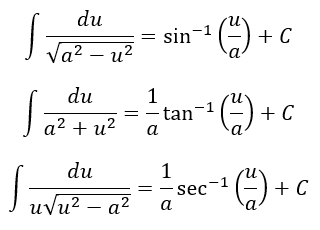Las funciones trigonométricas relacionan un ángulo de un triángulo rectángulo con las proporciones de las longitudes de dos lados, al conocer el ángulo podemos calcular la proporción de dos lados cualesquiera de un triángulo rectángulo. Estas funciones son seno, coseno, tangente, cotangente, secante y cosecante. Algunas de estas funciones están escritas en términos de otras funciones y pueden escribirse en forma compleja usando la fórmula de Euler:
Podemos memorizar las proporciones o calcularlas en base a su compleja definición siempre que los ángulos se escriban en radianes en lugar de grados.
En matemáticas hasta ahora, hemos visto que cada operación tiene múltiples enfoques y la memorización es un buen atajo pero no una herramienta imprescindible para hacer las operaciones. Otra propiedad importante de las matemáticas es que la mayoría de las operaciones (las que hemos cubierto hasta ahora) son reversibles. Puedes ir y venir y aprender cosas nuevas al respecto. Las operaciones que son reversibles se consideran tener una operación inversa.
Ya conocemos las operaciones inversas. Por ejemplo, la suma y la resta son operaciones inversas entre sí. La idea es la misma en trigonometría. Las funciones trigonométricas inversas hacen lo contrario de las funciones trigonométricas "normales". En general, si conoce la relación trigonométrica pero no el ángulo, puede usar la función trigonométrica inversa correspondiente para encontrar el ángulo.
¡Alerta de malentendidos!
La expresión sin-1(x), no es lo mismo que 1/sin(x). En otras palabras, el −1 no es un exponente. En cambio, simplemente significa función inversa. Otra forma de representar las funciones trigonométricas inversas es con el uso del prefijo arc- que posee la misma connotación que -1 (sin-1 = arcsin).
Dado que ninguna de las seis funciones trigonométricas es uno a uno, deben estar restringidas para tener funciones inversas. Por lo tanto, los rangos de resultados de las funciones inversas son subconjuntos de los dominios de las funciones originales.
|
Nombres
|
Notación
|
Definición
|
Rango en radianes
|
|
arco seno
|
y = arcsin (x)
|
x = sin (y)
|
- π/2 <y < π/2
|
|
arco coseno
|
y = arccos (x)
|
x = cos(y)
|
0 < y < π
|
|
arco tangente
|
y = arctan (x)
|
x = tan(y)
|
- π/2 < y < π/2
|
|
arco cotangente
|
y = arccot (x)
|
x = cot(y)
|
0 < y < π
|
|
arco secante
|
y = arcsec (x)
|
x = sec(y)
|
0 < y < π/2 ó π/2
< y < π
|
|
arco cosecante
|
y = arccsc (x)
|
x = csc(y)
|
- π/2 < y < 0 ó
0< y < π/2
|
Ahora que entendemos qué son las funciones trigonométricas inversas, veamos sus propiedades derivadas e integrales.
- Si f(x) y g(x) son funciones inversas entre sí (f(g(x)) = x y g(f(x)) = x), entonces la derivada g'(x) se puede obtener usando la siguiente fórmula.
En el caso del seno inverso, tenemos.
Esta no es una fórmula muy útil. Veamos si podemos conseguir una fórmula mejor. Comencemos recordando la definición de la función seno inversa.
Usando la primera parte de esta definición, el denominador en la derivada se convierte en,
Ahora podemos aplicar
Usando la segunda parte de la definición de la función seno inversa, el denominador se convierte en.
Poniendo todo esto junto, hemos encontrado la derivada para el arco seno.
Aplicamos el mismo método para encontrar todas las demás derivadas y las compilamos en una tabla.
Pero, ¿y si la función inversa tiene una función de x en lugar de un valor como u(x)? ¿Cómo afectaría esto a la derivada?
Lo bueno es que el cambio no es tan grande simplemente tenemos que aplicar la regla de la cadena. Para ver esto, podemos reescribir las fórmulas anteriores en una más general para ver cómo se verán afectadas.
Sea u = u(x). las derivadas de las funciones trigonométricas inversas con respecto a x son.
Ahora las derivadas no son solo para valores de x sino para todo tipo de funciones que dependen de x. Ahora que conocemos las derivadas, podemos usarlas para encontrar integrales del mismo tipo.
Sea a cualquier número distinto de cero y u una función de x.
Ahora lo más importante es poder reconocer este patrón con otras funciones. Examinemos algunos ejemplos.
Sea u2
= x2 à
u = x y du = dx; a2 = 16 à a = 4.
Sea u2
= 4x2 à
u = 2x reescribiendo x = u/2 and du = 2dx; a2
= 1 à
a = 1.
¿Qué pasa con una integral de esta forma?
Para resolver este problema, utilizamos una técnica llamada integración por partes que aún no hemos explorado. Entonces, por ahora lo mantendremos en espera hasta que expliquemos esta técnica y haremos ejemplos de estas funciones inversas.
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
También pueden seguir nuestro otro blog si les
interesa aprender sobre el interesante mundo de la física.