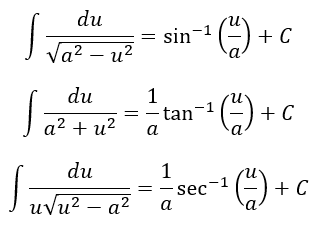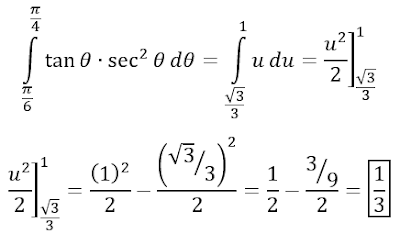Las funciones trigonométricas relacionan un ángulo de un triángulo rectángulo con las proporciones de las longitudes de dos lados, al conocer el ángulo podemos calcular la proporción de dos lados cualesquiera de un triángulo rectángulo. Estas funciones son seno, coseno, tangente, cotangente, secante y cosecante. Algunas de estas funciones están escritas en términos de otras funciones y pueden escribirse en forma compleja usando la fórmula de Euler:
|
Nombres |
Notación |
Definición |
Rango en radianes |
|
arco seno |
y = arcsin (x) |
x = sin (y) |
- π/2 <y < π/2 |
|
arco coseno |
y = arccos (x) |
x = cos(y) |
0 < y < π |
|
arco tangente |
y = arctan (x) |
x = tan(y) |
- π/2 < y < π/2 |
|
arco cotangente |
y = arccot (x) |
x = cot(y) |
0 < y < π |
|
arco secante |
y = arcsec (x) |
x = sec(y) |
0 < y < π/2 ó π/2
< y < π |
|
arco cosecante |
y = arccsc (x) |
x = csc(y) |
- π/2 < y < 0 ó
0< y < π/2 |
- Si f(x) y g(x) son funciones inversas entre sí (f(g(x)) = x y g(f(x)) = x), entonces la derivada g'(x) se puede obtener usando la siguiente fórmula.
Sea u2
= x2 à
u = x y du = dx; a2 = 16 à a = 4.
Sea u2
= 4x2 à
u = 2x reescribiendo x = u/2 and du = 2dx; a2
= 1 à
a = 1.
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden seguir nuestro otro blog si les
interesa aprender sobre el interesante mundo de la física.
- Facebook: https://www.facebook.com/JMDFisica
- Blogger: jmdfisica.blogspot.com