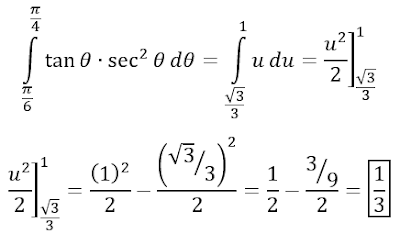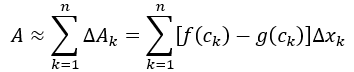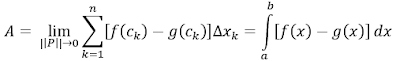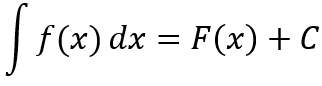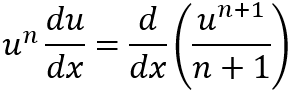Sigamos con otro ejemplo.
- Teorema: Si g’ es continua en el intervalo [a, b] y f es continua en el rango de g(x) = u, entonces
Sea
u = x3 +1, du = 3x2 dx
Cuando
x = -1, u = (-1)3 + 1 = 0
Cuando
x = 1, u = (1)3 +1 = 2
Así
que los nuevos límites de la integral son.
¿Qué método es mejor? En general, es mejor conocer ambos métodos y usar el que parezca mejor en ese momento, ya que cada integral es diferente y puede requerir diferentes enfoques.
Ejemplo 2 Evaluar
Sea
u = tan θ, du = sec2 θ dθ
Cuando
θ = π/4, u = tan(π/4) = 1
Cuando
θ = π/6, u = tan(π/6) = √3/3
Este teorema tiene otra implicación importante. Simplifica el cálculo de integrales definidas de funciones pares e impares en un intervalo simétrico [-a, a]. Un intervalo simétrico es fácil de detectar debido a la distribución de puntos.
Sea f continua en el intervalo simétrico [-a, a]
Si f es par, entonces .
Si f es impar, entonces
Puedes practicar para encontrar la prueba de esta afirmación usando la sustitución u y dividiendo la integral en dos regiones: a ≤ x ≤ 0 y 0 ≤ x ≤ a.
- Evaluar
y1 – y2
= f (x) – g (x)
Para ver cuál debería ser la integral, usamos la misma técnica que usamos cuando definimos la integral. primero aproximamos la región con n rectángulos verticales basados en una partición P = {x0, x1, …, xn} de [a,b]. el área del k-ésimo rectángulo es.
∆Ak = Altura × ancho = [f (ck ) – g(ck )]∆xk
Al sumar áreas de los n rectángulos, creamos nuestra suma de Riemann para aproximar el área.
- Si f y g son continuas con f(x) ≥ g(x) a lo largo de [a, b], entonces el área de la región entre las curvas es la integral de (f – g) de a a b.
- Encuentre el área de la región limitada arriba por la curva y = 2e-x + x, abajo por la curva y = ex/2, a la izquierda por x = 0 y a la derecha por x = 1.
- Encuentra el área de la región encerrada por la parábola y = 2 – x2 y la recta y = -x
- Encuentre el área en el primer cuadrante que está delimitada por la función y = √x y y = x – 2.
Puede apreciar que se tomaron muchos pasos para resolver este problema.
y
= √x à
x = y2; y = x – 2 à x = y + 2
Como las variables en este caso han sido
invertidas, límite de la derecha x = y + 2 mientras que el límite de la
izquierda es x = y2; el límite inferior de integración es c = 0 mientras
que el límite superior debemos encontrarlo.
El límite superior es d = 2 ya que -1
esta fuera del intervalo permitido. Ahora si podemos construir nuestra integral
y resolverlo.
Como podemos ver obtenemos el mismo valor
para el área ya que estamos trabajando el mismo problema, pero fue mucho mas fácil,
es decir que hay casos donde la integración de una variable es más simple que
la otra. Esto es muy importante a recordar pues será útil en integraciones de múltiples
dimensiones más adelante.
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden seguir nuestro otro blog si les
interesa aprender sobre el interesante mundo de la física.
- Facebook: https://www.facebook.com/JMDFisica
- Blogger: jmdfisica.blogspot.com