Hasta
ahora hemos visto las formulas para calcular el perímetro y el área de
triángulos y cuadriláteros regulares pero de forma general (para un polígono de
n lados) las reglas no siempre son iguales.
En el caso del perímetro solo debemos medir la distancia de cada lado y sumarlas. Así obtenemos la formula
Que se aplica para n lados de un polígono, no importa si este sea regular o irregular, el perímetro es calculado directamente. Esta simplicidad nos permite calcular el perímetro de figuras geométricas no regulares como la siguientes.
Ahora
podemos calcular el perímetro.
Este
tipo de figuras irregulares tienen la particularidad de que pueden ser
aproximadas completando su figura, es decir, buscando la figura geométrica
regular más próxima a ellas y calculado ese perímetro. En el caso del ejercicio
anterior esta figura es bastante parecía a un rectángulo así que si calculamos
el perímetro de un rectángulo con las mismas dimensiones tenemos.
Pero
no siempre es el caso. Así que es mejor calcularlo de la forma correcta. Veamos
otro ejemplo.
Si
aproximamos a figura geométrica a un rectángulo tenemos que nuestro perímetro
es
P = 2(15) + 2(6)
P = 42 in
Sin
embargo si calculamos el perímetro alrededor.
La
respuesta es muy diferente. Esta diferencia esta en si la figura es cóncava o
convexa. La primera figura se asemeja a una figura convexa y la segunda es una
figura cóncava.
El
área por otro lado es un poco mas complicado. Como el área determina la
cantidad de superficie encerrada, su resultado siempre nos da dos dimensiones,
así que siempre que calculamos el área estamos multiplicando dos dimensiones
(por lo general estas dimensiones son el largo (L) y el ancho (w)).
Entre
las áreas que hemos explorado hasta ahora se encuentran las siguientes
ecuaciones.
Cuadrado
Rectángulo
Paralelogramo
Triangulo
Trapecio
Ya hemos mencionado de figuras geométricas regulares pero no le hemos dado una definición. Los polígonos regulares son aquellos que todos sus lados y ángulos son iguales. De los triángulos, el triángulo equilátero es un polígono regular y de los cuadriláteros, el cuadrado es un polígono regular. Estos tienen la particularidad de que su perímetro se puede calcular conociendo un solo lado con la formula P = nL, donde n indica el número de lados. De tal forma que podemos encontrar el área de estas figuras con tan solo conocer el valor de un lado y su apotema. La apotema es la menor distancia entre el centro y cualquiera de los lados y siempre es perpendicular a dicho lado.
La apotema la podemos calcular.
Para polígonos regulares todos los ángulos miden lo
mismo, así que.
El área de un polígono regular se obtiene con la
siguiente formula.
Donde P es el perímetro y a es la apotema. el valor de
uno de los lados permite calcular el perímetro pues todos los lados miden lo mismo.
Ejemplo. Obtén el área de un hexágono regular si su
apotema es 2.6 cm y uno de sus lados mide 3 cm.
Como la figura es un hexágono esta tiene 6 lados así que su perímetro es
Ahora que conocemos el perímetro podemos calcular el área.
Recuerden que las unidades son al cuadrado.
¿Qué tal si tenemos una figura irregular y queremos calcular su área como la figura A? O queremos ser selectivo en el cálculo del área como la figura B?
En el caso de la figura B podemos encontrar el área de
la región sombreada sustrayendo el área del objeto y el área adjunta.
Con esto ya tenemos un mejor entendimiento de como
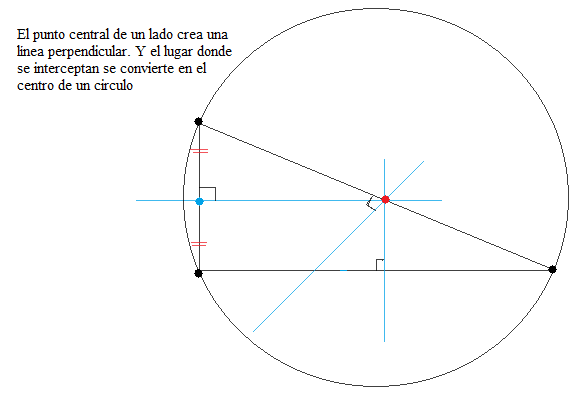
trabajar problemas del área y el perímetro. En la próxima publicación estaremos
hablando sobre el circulo y con esto cerraremos el tema de la geometría por
ahora. Los resultados a los ejercicios anteriores los dejare aquí debajo.
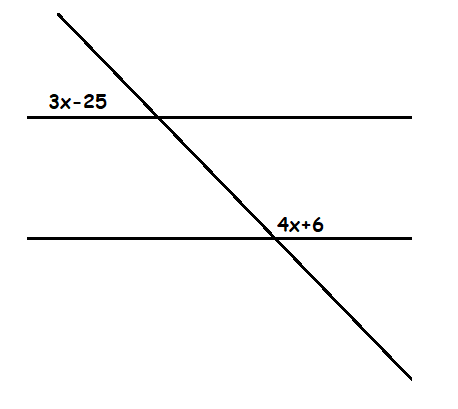
Encuentre el valor de todos los ángulos.
Primero quisiera nombrar todos los lados para poder usar las propiedades de las líneas transversales.Ahora si podemos decir que los ángulos F y H son congruentes al igual que los ángulos A y C. también podemos decir que los ángulos C y F son ángulos consecutivos y su suma es igual a 180º con lo cual podemos encontrar su valor.
El ángulo F es igual a
El ángulo C es igual a
La suma de estos dos ángulos es ≈ 180º pues el numero ha sido redondeado.
Ahora bien el ángulo A, C, E y G son congruentes y tienen la misma medida. De igual forma los ángulos B, D, F y H son congruentes y miden lo mismo.
Encuentre los ángulos internos que faltan en los siguientes triángulos.
En a figura A podemos encontrar el ángulo interno de
forma fácil.
En la figura B tenemos un triángulo rectángulo.
Sabemos que uno de los ángulos internos en un triángulo rectángulo es 90 º.
En la figura C es un poco más complicado ya que
tenemos un solo ángulo interno y tenemos el valor de los lados del triángulo.
Podemos usar la ley del seno para encontrar uno de los ángulos y de ahí
encontrar el ángulo interior restante.
Pero el rango del seno no permite números mayores que 1. Si comprobamos el valor de la altura tenemos que.
Si comparamos la altura con el otro lado vemos que h
> 5, esto no debería ser pues la hipotenusa debe ser el lado mas largo. Por
lo tanto decimos que este triangulo no tiene solución o no es posible.
Encuentre el área en los siguientes cuadriláteros.
La formula para calcular el área de un cuadrado es
bastante simple.
En el caso del rectángulo tenemos el valor de la
diagonal y necesitamos encontrar el valor del lado restante. Para ello podemos
aplicar el teorema de Pitágoras.
Ahora si podemos calcular el área
Ahora
pueden seguirnos y contactarnos a través de Facebook, Twitter y correo
electrónico.
- Facebook:
https://www.facebook.com/AprendeMatematicasJMD
- Twitter:
@JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden
seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de
la física.
- Facebook:
https://www.facebook.com/JMDFisica
- Blogger:
jmdfisica.blogspot.com