Tal vez la figura geométrica más usada hoy son los cuadriláteros; Desde juegos de mesa, la misma mesa, espejos, celulares puertas y ventanas y muchas otras cosas están construidas en forma de cuadriláteros. La palabra cuadrilátero significa cuatro lados, ya que la palabra “-latero” se refiere a laterales o lados y “cuadro- “se refiere a cuatro. Los cuadriláteros se clasifican y se definen generalmente por sus propiedades.
Paralelogramos: es un cuadrilátero cuyos lados
opuestos son paralelos.
Rectángulo: es un paralelogramo con cuatro ángulos
internos recto.
Cuadrado: un rectángulo con sus cuatro lados
de igual tamaño.
Rombo: es un paralelogramo con los lados
de igual tamaño.
Trapecio: con dos lados paralelos
exactamente.
Elementos generales de un cuadrilátero
- Un segmento de recta que une dos vértices no consecutivos se denomina diagonal. Todos los cuadriláteros contienen dos diagonales.
- La suma de sus ángulos internos es 360º.
- Si un cuadrilátero está inscrito en una circunferencia la suma de la medida de sus ángulos opuestos es igual a 180º.
- El área de un cuadrilátero inscrito se obtiene
usando la formula
, donde a, b, c, d son los lados y p es el semiperímetro.
Rectángulos
Puertas,
ventanas, celulares, fotos y hasta el papel moneda son ejemplos de un rectángulo.
Los rectángulos tienen varias características.
- Todos los ángulos internos son rectos.
- Los lados opuestos son paralelos.
- Los lados opuestos tienen la misma longitud.
- Las diagonales tienen la misma longitud.
- Las diagonales se interceptan en el punto medio.
Vamos a
usar estas características para resolver el siguiente problema.
Problema: El cuadrilátero ABCD es un rectángulo, encuentre las siguientes medidas.
a)
Como
es un rectángulo, el ángulo 
b)
La
longitud del lado AB no es dada como 8 m.
c)
La
longitud de la diagonal AC la podemos encontrar usando el teorema de Pitágoras
o usando la idea que “Las
diagonales se interceptan en el punto medio” y que “Las diagonales tienen la
misma longitud” la medida del segmento EB es 5 m y la medida del segmento DB =
2EB à 10
m así que la diagonal AC es 10 m.
d)
La
medida DE es igual a la medida EB es decir 5 m.
Podemos
convertir un paralelogramo en un rectángulo si el cumple los siguientes
criterios.
- Si un paralelogramo tiene un ángulo recto.
- Si las diagonales de un paralelogramo son congruentes.
Ejemplo. Un carpintero quiere construir un
cobertizo con una base de 10 ft por 8 ft. ¿Cómo se puede asegurar que la
fundación tiene cuatro ángulos rectos?
Una de las
propiedades de los rectángulos es que sus diagonales tienen la misma medida. Si
podemos mostrar que las diagonales son congruentes, entonces podemos decir que
la base está en forma rectangular y sus ángulos internos son rectos.
Para ello
vamos a formar un paralelogramo cuyos lados opuestos tengan la misma longitud,
luego podemos usar una cinta métrica para medir las diagonales. Si ambas miden
lo mismo entonces nuestro paralelogramo es un rectángulo.
Trapecio
Es
importante no confundir un trapecio y un trapezoide, ya que la definición de
estos puede variar dependiendo de la región donde se habla el idioma, pero las
matemáticas definen un trapecio como un cuadrilátero que tiene un par de lados
paralelos mientras que un trapezoide es un cuadrilátero irregular sin lados
paralelos (la figura A corresponde a un trapecio y la figura B a un
trapezoide). En un trapecio encontramos los siguientes elementos.
- Sus lados paralelos se llaman base. Existe una base mayor y una base menor, estas son determinadas por su tamaño.
- La altura del trapecio es un segmento que una perpendicularmente las dos bases.
- El segmento que une los puntos medios de lados no paralelos se denomina mediana. La longitud de la mediana de un trapecio es igual a la suma de la longitud de sus bases dividida entre dos.
- La altura puede calcularse en función a las bases y los lados mediante la siguiente ecuación.
Podemos
imaginar un trapecio como dos líneas paralelas siendo cortadas por líneas transversales.
Como los
ángulos ∠A y ∠D son ángulos suplementarios de
forma similar podemos decirlo con el otro lado y los ángulos ∠B y ∠C, lo que nos permite crear el
enunciado “en un trapecio siempre hay dos pares de ángulos suplementarios.”
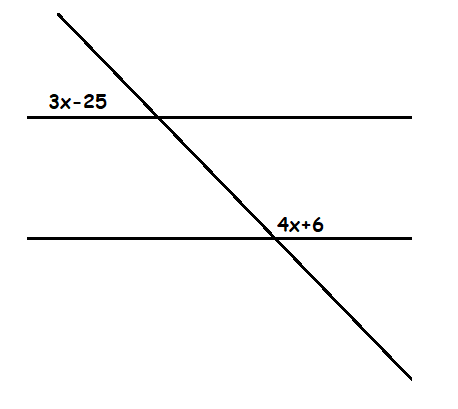
Ejemplo. Encuentre el valor de los ángulos x
e y.
Como son ángulos suplementarios la suma de sus ángulos es igual a 180°.
Si los
lados no paralelos del trapecio tienen la misma longitud entonces la figura
geométrica se conoce como trapecio isósceles. El trapecio DEFG en la figura A
es un trapecio isósceles pues DG ≅ EF. En un trapecio como este podemos decir que
ambos pares de ángulos con respecto a sus bases son congruentes. ∠D ≅ ∠E y ∠F ≅ ∠G.
Cuadrado
El más simple de los cuadriláteros. Compuestos de cuatro lados congruentes y cuatro ángulos internos rectos. Esta figura geométrica es considerada una figura regular. Sus diagonales se bisecan en el baricentro y estas son perpendiculares entre si creando cuatro ejes de simetría.
que se
obtiene de la simplificación del teorema de Pitágoras. Como todos los lados son
congruentes, su perímetro se puede calcular como 4a y su área como a2.
Paralelogramo
Un
paralelogramo es un cuadrilátero cuyos pares de lados opuestos son iguales y
paralelos. Por su definición es el cuadrilátero más común y extenso ya que por
definición hay otros cuadriláteros que son clasificados como paralelogramos
como son el cuadrado, rombo, rectángulo y romboide.
Existe una
ley geométrica que relaciona los lados de un paralelogramo con sus diagonales
llamada ley de los paralelogramos. Esta dice que la suma del cuadrado de los
lados es igual a la suma del cuadrado de las diagonales.
Puesto que
los lados son iguales dos a dos, se puede simplificar.
Con esto
concluimos el tema de los cuadriláteros. Existen aun muchos mas ejemplos que
podemos presentar y figuras irregulares que podemos trabajar pero esto lo
dejaremos para otra ocasión. Aquí les dejo algunos ejercicios de practica para
las líneas transversales, triángulos y cuadriláteros. Espero les sea de ayuda.
Nuestro próximo tema será sobre área y perímetro. Preguntas y sugerencias la
pueden escribir en la sección de comentarios o enviarlas directamente al
correo. Recuerden que el propósito de esto es de ayudarlos en todo lo posible.
Encuentre
el valor de todos los ángulos.
Encuentre los
ángulos internos que faltan en los siguientes triángulos.
Encuentre
el área en los siguientes cuadriláteros.
Ahora pueden seguirnos y contactarnos a
través de Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Twitter:
@JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden
seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de
la física.
- Facebook:
https://www.facebook.com/JMDFisica
- Blogger: jmdfisica.blogspot.com
No hay comentarios.:
Publicar un comentario