Hasta
ahora ya hemos estudiado las rectas y las propiedades que surgen de la
interacción de dos o más de ellas. En esta sección trataremos de las figuras
planas que se forman cuando estas rectas forman un espacio cerrado. Estas
figuras formadas por secuencias de segmentos de rectas que forman un espacio
cerrado son llamados polígonos.
Un polígono es una figura geométrica plana que encierra una región en el plano. Un plano es un objeto que posee dos dimensiones con infinitos puntos y rectas. Un plano queda definido si contiene:
- Tres puntos no alineados.
- Una recta y un punto exterior a ella.
- Dos rectas paralelas o dos rectas que se cortan.
Un plano suele ser nombrado usando una letra del alfabeto griego. en estos planos es donde construimos nuestros polígonos bidimensionales.

Plano nombrado por la letra π (pi).
En
un polígono se distinguen varios elementos geométricos como son:
Lados: son cada uno de los segmentos de
recta que conforman el polígono.
Vértices: es el punto de intersección de dos lados
consecutivos del polígono.
Diagonales: es un segmento de recta
que une dos vértices no consecutivos del polígono.
Ángulos interiores: son los ángulos
formados por los lados consecutivos dentro de la región cerrada del polígono
Ángulos exteriores: son los ángulos
formados externamente al polígono, por uno de sus lados y la prolongación del
lado consecutivo.
Existen
otros elementos que se pueden identificar en un polígono como son el centro
y apotema.
Triángulos
Un
polígono se forma al unir segmentos de recta de forma que no dos segmentos se interceptan,
excepto en sus puntos final. Como un polígono contiene un espacio cerrado, el
mínimo numero de lados que forma un polígono es 3 y esta forma es conocida como
triangulo (tres ángulos). Los lados de un triángulo son nombrados usando letras
mayúsculas mientras que la longitud de los lados es denotada por letras
minúsculas, los ángulos internos son nombrados por lo general usando la letra
griega theta, θ, pero cualquier letra puede ser usada.
Un triángulo puede ser clasificado según la longitud de sus lados o según el tamaño de sus ángulos internos.
- Según la longitud de sus lados:
Triangulo equilátero: la longitud de los tres lados es la misma, creando así un triángulo cuyos ángulos internos miden 60° ó π/3 radianes
Triangulo isósceles: dos lados del triangulo
tienen la misma longitud. Los ángulos opuestos a estos lados tienen la misma
medida.
Triangulo escaleno: la longitud de todos
los lados es diferente y los ángulos internos también son todos diferentes.

Las líneas indican cuales lados son iguales. En la parte C estas indican que son diferente.
- Por la amplitud de sus ángulos:
Triangulo acutángulo: todos sus ángulos
internos son agudos.
Triangulo rectángulo: uno de sus ángulos internos es un ángulo recto, es decir de 90°.
Triangulo obtusángulo: dos de sus lados forman
un ángulo obtuso.
La
suma de los ángulos internos es dada por la fórmula 180°(n-2) donde “n” es el
numero de lados. Como un triangulo tiene 3 lados, la suma de sus ángulos
internos es 180°.
Propiedades
Dentro
de un triángulo podemos trazar rectas que concurren en un punto, creando así
propiedades interesantes.
- Una línea que une cada vértice con el centro de su lado opuesto se llama mediana. El punto de intersección de las medianas es conocido como baricentro. Este también es el centro de equilibrio del triángulo.
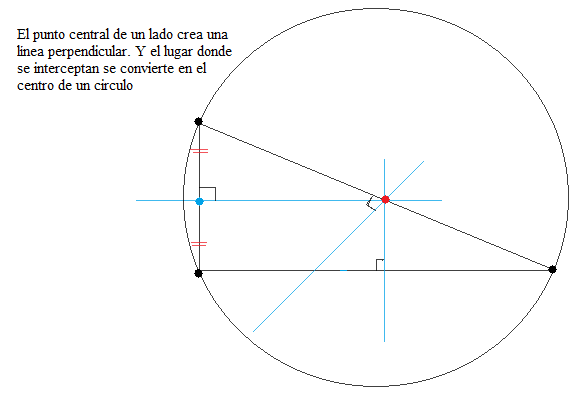
- Existen también líneas que son perpendiculares al punto central de cada lado, estos se llaman mediatrices y su punto de intersección es el circuncentro. El circuncentro coincide con el centro de la circunferencia que pasa por los tres vértices del triángulo.
- Una línea que divide cada ángulo interno en dos ángulos de la misma medida se llama bisectriz. El punto de intersección de las bisectrices se conoce como incentro. Este punto permite trazar una circunferencia inscrita y tangente a todos los lados del triángulo.
- Podemos trazar líneas que desde un vértice hasta el lado opuesto que sean perpendiculares. Llamamos a estas líneas altura el punto donde se interceptan es el ortocentro. Cada altura divide el triángulo en dos triángulos rectángulos.
Existen
métodos para calcular la longitud de un lado y la medida de un ángulo. Para
resolver triángulos en general se suele utilizar los teoremas del seno y del
coseno pero en el caso especial de triángulos rectángulos utilizamos el teorema
de Pitágoras.

Triangulo de referencia para las definiciones.
El
teorema de Pitágoras afirma que en todo triangulo rectángulo el cuadrado de la
hipotenusa es igual a la suma de los cuadrados de los catetos. Si no estas
familiarizado con estos nombres los catetos son los lados del triangulo que
forma el ángulo recto mientras que la hipotenusa es el lado opuesto al ángulo
recto. Este teorema se puede escribir como una ecuación.
Algunos
datos curiosos sobre este teorema es que el lado de la hipotenusa siempre será
el lado mas largo de los tres; podemos crear un triángulo rectángulo dentro de
cualquier triangulo usando su altura y el teorema de Pitágoras para determinar
la longitud de sus lados.
Una
de las grandes ventajas de este teorema es que ayudo mucho en la construcción
de las conocidas funciones trigonométricas [seno (sen), coseno (cos), tangente
(tan), cotangente (cot), secante (sec) y cosecante (csc)].
Los
triángulos son los únicos polígonos que siempre son convexos pues ninguno de
sus ángulos internos puede ser mayor que 180 grados.
Los
lados de un triangulo son proporcionales a los senos de los ángulos opuestos.
Esto aplica para cualquier triangulo y es conocido como el teorema del seno.
El
cuadrado de un lado es igual a la suma de los cuadrados de los otros menos el
doble del producto de estos lados por el coseno del ángulo comprendido. Esto
también se conoce como teorema del coseno.
Congruencia
de los triángulos
Dos
triángulos son congruentes si hay una correspondencia entre sus vértices de
forma que los lados y el ángulo del vértice sean congruentes con el otro. Esto
permitió la postulación de la congruencia y en si el teorema de congruencia.
Postulados
- LAL (lado, ángulo, lado): dos triángulos son
congruentes si dos de sus lados en uno tienen la misma longitud que dos lados
del otro y el ángulo comprendido entre esos lados tienen la misma medida.
- ALA (ángulo, Lado, ángulo): dos triángulos
son congruentes si dos ángulos internos y el lado comprendido entre ellos
tienen la misma medida y longitud.
- LLL (lado, lado, lado): dos triángulos son
congruentes si cada lado de un triangulo mide lo mismo que los correspondientes
del otro triangulo.
- Teorema de congruencia (AAL) dos triángulos
son congruentes si dos ángulos y un lado no comprendido entre los ángulos
tienen la misma medida.
Área
y Perímetro
Finalmente
en el mundo de los polígonos existen dos conceptos que nos permite determinar
que tanta superficie es cubierta por el polígono y la distancia alrededor de la
figura, esta son el área y el perímetro.
El
perímetro es la suma de todos los lados de un polígono. Tan simple como
eso. Simplemente medimos todos los lados y los sumamos y el resultado es el
perímetro. Es un concepto bastante usado a la hora de construir una cerca, un
muro, o un puente ya que el perímetro nos da una idea de cuanto material será
requerido para cubrir una superficie especificada. Así que la medida del
perímetro es unidimensional.
El
área nos permite medir la extensión de una superficie, que tanto terreno
ha sido cercado, o la extensión de la superficie que se encuentra dentro de una
pirámide. Para ello necesitamos conocer la longitud de dos dimensiones de esta
superficie, por lo general su largo y su ancho pero dos cualesquiera funcionan.
El área de
un triángulo es igual al semiproducto entre la longitud de una
base y la altura relativa a esta:
Donde b es
la base del triángulo y h es la altura correspondiente a la base. (se
puede considerar cualquier lado como base)
Si
el triángulo es rectángulo, la altura coincide con uno de los catetos, con
lo cual el área es igual al semiproducto de los catetos:
Donde a y b son
los catetos.
Si se
conoce la longitud de sus lados, se puede aplicar la fórmula de Herón en
vez de determinar la altura.
Donde a, b, c son
los valores de las longitudes de sus
lados, s = ½ (a + b + c) es el semiperímetro del
triángulo.
Si
el triángulo es equilátero, el área es igual a un cuarto del cuadrado de
un lado por la raíz cuadrada de 3:
Esto
cubre las partes más importantes de los triángulos. Para la próxima publicación
trataremos sobre cuadriláteros y posiblemente podremos algunos ejercicios para
practicar los triángulos y los cuadriláteros. Si tienen alguna pregunta como
siempre pueden dejarla en la sección de los comentarios. Sugerencias también
son aceptadas así que no duden en escribir.
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden
seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de
la física.
- Facebook: https://www.facebook.com/JMDFisica
- Blogger: jmdfisica.blogspot.com