En la previa publicación tratamos el tema de las líneas y los ángulos. Para entender las propiedades de las líneas transversales tenemos dos definiciones extras que agregar.
Tres o más líneas son concurrentes
si son interceptadas en un solo punto, es decir si varias líneas se cruzan en
el mismo punto entonces estas líneas son llamadas concurrentes. Un gran ejemplo
de esto es la rotonda donde se encuentra el arco del triunfo en parís. El arco es el punto o vértice donde las
diferentes calles se interceptan haciendo que estas calles sean concurrentes unas
con otras.
Existen ángulos que comparten un
lado y un vértice en común con otros. Estos ángulos son llamados consecutivos
como su nombre indica están uno al lado del otro. Si los ángulos consecutivos
son suplementarios, es decir su suma es igual a 180° entonces
decimos que son ángulos adyacentes.
En el ejemplo B aunque los ángulos son consecutivos
no son adyacentes pues no suman 180°.
Una línea transversal es aquella que
atraviesa dos líneas. Supongamos que tenemos dos líneas paralelas y estas son
interceptadas por una tercera línea. Esta tercera línea es la línea transversal.
Una línea transversal es muy
importante para el estudio de los ángulos ya que nos permite ver propiedades
que no se ven a simple vista. Veamos un ejemplo.
- Como se puede apreciar la línea
transversal crea ocho diferentes ángulos con las paralelas. Cuatro entre cada
paralela. Los ángulos ∠1, ∠2, ∠3 y ∠4 crean una circunferencia completa
por lo que su suma es igual a 360°. Lo mismo con los ángulos ∠5, ∠6, ∠7 y ∠8.
- Los ángulos ∠1 y ∠2 son consecutivos y su suma es 180°, por lo tanto
son ángulos adyacentes. Lo mismo podemos decir de las combinaciones de los
ángulos ∠1 y ∠3, ∠2 y ∠4, ∠3 y ∠4, ∠5 y ∠6, ∠5 y ∠7, ∠6 y ∠8, ∠7 y ∠8.
- Los ángulos ∠3, ∠4, ∠5 y ∠6 se encuentran entre las paralelas
y son llamados ángulos interiores.
- Los ángulos ∠1, ∠2, ∠7 y ∠8 se encuentran en el lado opuesto
de las paralelas y son llamados ángulos exteriores.
- Los ángulos ∠3 y ∠6 están dentro de las paralelas pero
en lados opuestos, por esta razón son llamados ángulos internos alternos. Los
ángulos ∠4 y ∠5 también se encuentran en lados
opuestos entre las paralelas y son ángulos internos alternos también.
- Los ángulos ∠1 y ∠8 se encuentran en la parte de
afuera de las paralelas y están en lados opuestos, por esta razón son llamados
ángulos alternos externos. Los ángulos ∠2 y ∠7 también cumplen este criterio.
- Existen también ángulos correspondientes. Estos están compuestos de un interno y un externo y deben estar en el mismo lado de las paralelas con respecto a la línea transversal y son congruentes, es decir iguales en su valor. Un ejemplo de esto son los ángulos ∠1 y ∠5.
- Existen ángulos internos cuya suma
es igual a 180°, estos son llamados ángulos internos
consecutivos. Los ángulos ∠4 y ∠6 son un ejemplo.
Existen ángulos que están en el lado opuesto del vértice uno con otro y su valor es el mismo, es decir son congruentes. Llamamos a estos ángulos verticales. Los ángulos ∠1 y ∠4 son un ejemplo así como los ángulos ∠2 y ∠3. Cabe denotar que estas propiedades en su mayoría son casos donde dos líneas paralelas son atravesadas por una transversal. En el caso de que las líneas no sean paralelas algunas de estas propiedades no serán iguales pero en el caso que lo sean solo necesitamos saber el valor o la expresión de uno de los ángulos y de ahí podemos derivar todos los demás valores.
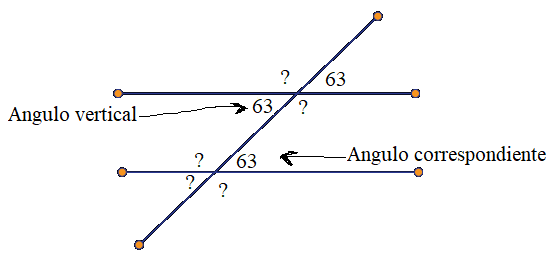
Usando las propiedades descritas
podemos inmediatamente determinar el valor del ángulo vertical que esta en el lado
opuesto del vértice y el ángulo correspondiente al ángulo dado y tenemos lo
siguiente.
Con esto podemos calcular los ángulos
adyacentes y con eso tendremos el resultado de todos los ángulos.
Pueden haber más de una línea
transversal creando así más o menos de cuatro ángulos internos. El valor de la
suma de los ángulos internos depende del número de lados disponibles y puede
ser calculado utilizando la formula (n-2)180 donde n es el numero de lados.
Esta formula es importante ya que describe el valor de la suma de los ángulos
internos en las figuras geométricas que estudiaremos en el futuro (es bastante
conocido que la suma de los ángulos internos de un triangulo es 180° pues un
triangulo tiene tres lados y usando la fórmula que así se describe vemos que es
correcto).
Convertir los siguientes ángulos.
135° a radianes
A pesar de que por lo general el valor de pi es de 3.14 prefiero dejar
ver a pi como una constante ya que esto hace que los cálculos sean más fáciles.
Usando la regla de tres.
3π/4 radianes a grados
El ejercicio anterior nos mostro que el valor de 3π/4 en grados es de
135°. Ahora voy a aplicar la regla de tres en reverso para confirmar que este
es así.
60° a radianes
2π/5 a grados
π/6 a grados
275° a radianes
¿Cuál es el ángulo complementario de 35°?
La suma de ángulos complementarios es igual a 90° así que para encontrar
el ángulo complementario debemos sustraer el ángulo dado a los 90°.
90° - 35° = 55°
El ángulo complementario de 35° es 55°.
¿Cuál es el ángulo suplementario de 76°?
La suma de ángulos suplementarios es igual a 180°, así que para
encontrar el ángulo suplementario debemos sustraer el ángulo dado a los 180°.
180° - 76° = 104°
El ángulo suplementario de 76° es 104°.
Dos ángulos son complementarios y sus ángulos miden 2x+5 y 3x-20.
¿Cuáles son los ángulos?
La suma de ángulos complementarios es igual a 90°. Aquí se nos dan dos
expresiones para los ángulos que debemos resolver. Podemos aplicar las mismas
ideas que en problemas anteriores para obtener una ecuación que nos permitirá
saber el valor de x. una vez conocemos ese valor podemos resolver las dos
expresiones para encontrar los valores de los ángulos.
A = 2x+5 y B = 3x-20
A = 2(21) + 5 = 42+5 = 47°
B = 3(21) – 20 = 63 – 20 = 43°
A + B = 90° → 45° + 43° = 90°