Sabemos que en matemáticas tenemos 2 clases de logaritmos: el logaritmo común y el logaritmo natural. El logaritmo natural, representado como ln, tiene como base la constante de Euler e con un valor aproximado de 2.718281828459. El logaritmo común, representado como log, tiene una base generalmente de 10 pero puede ser cualquier número. Aunque sus bases difieren, sus propiedades se mantienen.
Log(A∙B)
= log(A) + Log(B)
Ln(A∙B)
= ln(A) + Ln(B)
Por ahora, mi preocupación está asociada con esto. Sus propiedades se aplican de la misma manera y, por lo tanto, las siguientes propiedades para explorar afectan ambos logaritmos por igual, pero para mi cordura y simplicidad usaré el logaritmo natural en lugar del logaritmo común.
La función ex es una función exponencial general cuya gráfica tiene una pendiente 1 cuando cruza el eje x. Su función inversa se llama logaritmo natural. El valor de este logaritmos se puede expresar como una integral de la forma.
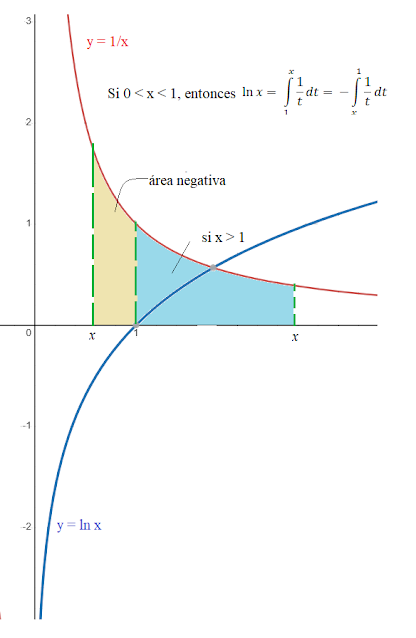
Si ln |x| para x ≠ 0, entonces.
Sea u = 3 + 2 sin θ; du = 2 cos θ
dθ, y cuando u(π/2) = 5; u(-π/2) = 1
Sea u = cos x; du = - sin x dx
Logaritmo con base a
Sea u = ln x; du = 1/x
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden seguir nuestro otro blog si les
interesa aprender sobre el interesante mundo de la física.
- Facebook: https://www.facebook.com/JMDFisica
- Blogger: jmdfisica.blogspot.com
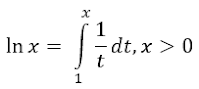








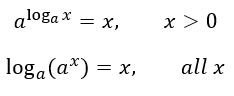







No hay comentarios.:
Publicar un comentario