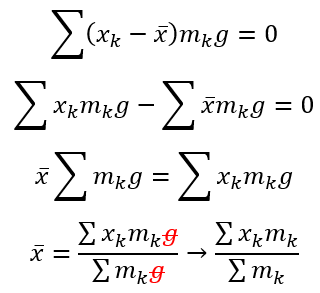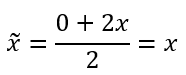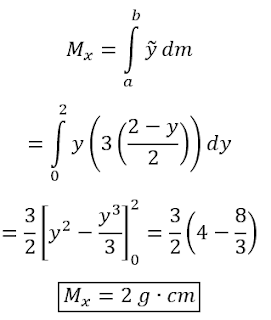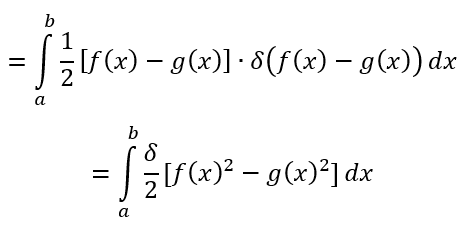En esta publicación discutiremos las matemáticas de dos términos de física. No vamos a entrar en detalles para explicar el significado de fórmulas o derivaciones de unidades que están más en el ámbito de una publicación de física. Si te interesa esto te sugiero que leas mi post sobre trabajo. En cambio, examinaremos el aspecto matemático del cálculo del trabajo.
Definimos Trabajo en la
vida cotidiana como una actividad que requiere esfuerzo muscular o mental. Sin
embargo, en ciencia los términos se refieren a una fuerza que actúa sobre un
cuerpo. Cuando un cuerpo se mueve una distancia d como resultado de la
acción de una fuerza F en la dirección del movimiento, eso es lo que
definimos como trabajo, y está representado por la ecuación.
La fuerza es una cantidad
vectorial y también lo es la distancia, lo que hace que esta operación sea más
similar al producto escalar de dos vectores, y el trabajo es una cantidad
escalar independiente de la dirección, esta fórmula solo nos dice el trabajo
donde también conocemos la magnitud de la fuerza aplicada. como la magnitud de
la distancia (los problemas relativos a los vectores se estudiarán en futuros
post). Si la fuerza aplicada varía a lo largo del camino, la fórmula debe ser
reemplazada por una fórmula integral. Como hemos visto antes, para que se
produzca este cambio, la cantidad variable (en este caso, la fuerza) debe ser
una función continua en un intervalo específico. Entonces, sea la fuerza una
función continua de la posición del objeto en el intervalo a ≤ x ≤ b.
Particionamos [a, b] y elegimos el punto arbitrario ck. La distancia
se define como ∆xk en xk-1 a xk, luego tomamos
el límite para obtener nuestra nueva expresión.
Este es el trabajo
realizado por una fuerza variable F(x) en la dirección del movimiento a
lo largo del eje x desde x = a hasta x = b. Usamos el eje
x para denotar una idea general de dirección, la fórmula funciona de la
misma manera en cualquier eje que elijamos.
Ejemplo.
¿Cuál es el trabajo
realizado por una fuerza F(x)
= 1/x2 que
mueve un objeto a lo largo del eje x
desde x = 1 hasta x = 10?
Este es un ejemplo muy
sencillo. Tenemos nuestra función de fuerza y nuestro intervalo; todo lo que tenemos
que hacer es ponerlos en la ecuación 2 y resolver.
Una cubeta de 7 lb se eleva del suelo al aire tirando de 25 pies de cuerda a una velocidad constante. La
cuerda pesa 0.06
ft/lb.
¿Cuánto trabajo se dedicó a levantar el balde y la cuerda?
Debemos hallar el trabajo
de levantar el balde y levantar la cuerda y sumarlos. Dado que el balde tiene
un peso constante, y esta es otra expresión para indicar la fuerza, el trabajo
realizado para levantar el balde solo es peso x distancia.
El peso de la cuerda varía
con la elevación de la cubeta porque hay menos cuerda colgando libremente, por
lo que la tasa de cambio de la longitud de la cuerda es 25 – x y su peso
(0.06) (25 – x), por lo que el trabajo realizado para levantar la cuerda
es.
El trabajo total para el balde y la cuerda combinados es.
Un buen ejemplo para
estudiar cómo actúa el trabajo es bombear líquidos desde un recipiente. La
dimensión del recipiente y el peso del líquido son los factores que afectan la
cantidad de trabajo que se necesitará para bombearlo. Imaginamos sacar el
líquido una losa horizontal delgada a la vez y aplicar nuestra ecuación de
trabajo a cada losa. Luego evaluamos la integral que conduce a que las losas se
vuelvan más delgadas y numerosas.
Veamos algunos ejemplos en
funcionamiento para obtener los pasos para resolver cualquier problema de
bombeo.
Tenemos la función y = 2x en el intervalo 0 ≤ x ≤ 5. Rotamos la función alrededor del eje y y obtenemos un cono con radio de x = ½ y. llenamos el cono con un peso líquido de
55
lb/ft3
hasta 2
pies de
la parte superior. ¿Cuánto trabajo se necesita para bombear el líquido hasta el
borde del tanque?
Este problema requerirá
mucha manipulación geométrica. Para empezar, imaginamos el líquido dividido en
finas láminas de volumen ∆V, por planos perpendiculares al eje y.
Tomamos una losa y encontramos una expresión para su trabajo y básicamente todo
lo que tenemos que hacer después de eso es agregar un número infinitesimal de
losas para obtener una aproximación del trabajo total. Luego, aplicando límites
a esto, obtenemos la solución que estamos buscando. El volumen de una sola losa
se encuentra usando la fórmula ∆V = π(radio)2(ancho).
Como sabemos la densidad
del líquido porque se dio en el enunciado, podemos usar esto para encontrar la
fuerza requerida para levantar la losa que es igual a su peso.
F(y)
= 55lb/ft3∆V
La distancia para levantar
esta losa al nivel del borde del cono es 10 – y (ya que el intervalo de
la función cubre 0 ≤ x ≤ 5 el valor máximo para y = 10). Ahora
que conocemos la fuerza y la distancia, podemos calcular el trabajo.
Para encontrar el trabajo
aproximado realizado levantando las n losas, usamos una suma de Riemann
Si tomamos el límite de la
suma de Riemann a medida que las losas se vuelven más delgadas, obtenemos la
integral.
Se utiliza un tanque
rectangular con la parte superior a nivel del suelo para recoger el agua de
escorrentía. Suponga que el agua pesa 62.4 lb/ft3. ¿Cuánto trabajo se necesita para vaciar
el tanque bombeando el agua de regreso al nivel del suelo una vez que el tanque
está lleno? Las dimensiones del tanque se dan en la figura.
Vayamos paso a paso para
comenzar con la fórmula del trabajo.
La fuerza la podemos
encontrar multiplicando el peso por el volumen.
Dado que el tanque tiene
forma rectangular, el volumen de una losa es el largo x ancho x grueso.
Por lo tanto, la fuerza es.
La distancia recorrida por
el bombeo del agua es.
Ahora tenemos todo para
encontrar el trabajo de bombear una losa.
Si sumamos todas las losas
y luego tomamos los límites a medida que se vuelven más delgadas y el número se
acerca al infinito, obtenemos la integral.
Centro de Masa
Muchos sistemas mecánicos
se comportan como si sus masas estuvieran concentradas en un solo punto. Este
punto nos permite calcular y predecir el movimiento incluso cuando su
movimiento parece tan complicado de calcular (tales predicciones que sucedan).
Desarrollaremos nuestro modelo matemático de centro de masa en etapas.
Comenzando con el examen de un sistema de distribución discreto. La
distribución de masas individuales m1, m2 y
m3 en un eje x unidimensional sostenido por un fulcro
en el origen.
El sistema estará en
equilibrio dependiendo de cuán grandes sean las masas y cómo estén dispuestas a
lo largo del eje x (algo así como un sube y baja). Cada masa mk
ejerce una fuerza hacia abajo mkg (el peso de la masa mk).
Cada fuerza puede girar el eje alrededor del origen en algo llamado torque (que
se mide multiplicando la fuerza mkg por la distancia firmada xk).
La suma de los pares mide la tendencia de un sistema a girar. Esta suma la
llamamos torque del sistema.
Fuerza
de torsión del sistema= τ = m1g.x1
+ m2g.x2 + m3g.x3
Si el sistema no está
balanceado, el torque hará que el sistema gire, pero si el sistema está
balanceado, los torques (neto) serán cero. Si factorizamos el término común,
notamos algo interesante sobre el torque.
g (m1x1
+ m2x2 + m3x3)
El torque es el producto de
una característica del entorno en el que reside el sistema (azul) y un número (rojo), característica del sistema que
permanece igual sin importar dónde se coloque el sistema. Esta constante se
conoce como el momento del sistema con respecto al origen. Es la suma de los
momentos de las masas individuales.
Ahora lo que nos interesa
es dónde podemos colocar el fulcro para hacer que el sistema se equilibre (el
punto x donde todos los torques suman cero).
El torque de cada masa en
esta ubicación especial es.
Aplicando nuestra condición
∑ τk = 0
Que es una ecuación que
podemos manipular para encontrar x̄.
Esta ecuación nos dice que
podemos encontrar x̄ dividiendo el momento del sistema por la masa total
del sistema. Este punto se llama centro de masa.
Ejemplo:
Un niño de 32 kg se sienta en un extremo de un sube y
baja de 2.5
m de
largo. ¿Dónde debe sentarse su padre de 71 kg para que el centro de masa esté en el
centro del sube y baja?
Dado que el niño está en un
extremo del sube y baja, tomamos el origen del sistema de coordenadas para
estar en la posición del niño (x1 = 0). La longitud total del
sube y baja es de 2.5 m, queremos que el centro de masa esté en el
centro del sube y baja, que está a la mitad de la distancia, que es 1.25 m,
pero tenemos que averiguar cuál será la distancia para su padre, así que
necesitamos resolver nuestra ecuación para encontrar esta distancia.
Masa Sobre Una Región Plana
Supongamos que tenemos una
colección finita de masas en el plano x-y con masa mk
en el punto (xk, yk). La masa del sistema es.
M = ∑mk
(4)
Cada masa mk
tiene un momento alrededor de cada eje. El momento de todo el sistema con
respecto a los dos ejes está determinado por el momento con respecto a cada
eje.
El momento sobre el eje
x de la partícula que puede girar libremente alrededor del eje x es
la masa de la partícula multiplicada por la distancia desde el eje x.
Mx
= ∑
mk
yk
(5)
El momento sobre el eje
y de la partícula que puede girar libremente alrededor del eje y es
la masa de la partícula multiplicada por la distancia desde el eje y.
My
= ∑
mk
xk
(6)
El centro de masa en cada
eje es la coordenada (x̄, ȳ).
(7)
Con esta elección, en lo
que respecta al equilibrio, el sistema se comporta como si todas las masas
estuvieran en un solo punto (x̄, ȳ), llamamos a este punto el centro de
masa del sistema.
Placas Planas Delgadas
En lugar de tener una masa centrada
en un punto, tenemos un área como una hoja o una placa plana delgada donde la
masa es continua y las fórmulas para el centro de masa contienen integrales en
lugar de sumas finitas.
Imagine que una placa
delgada que ocupa una región en el plano xy se corta en tiras delgadas
paralelas a uno de los ejes. El centro de masa de una de las tiras es (x̃, ỹ)
y la masa de la tira ∆m la tratamos como si estuviera
concentrada en (x̃, ỹ), el momento de la tira es, por lo tanto.
My
= x̃ ∆m
Mx
= ỹ ∆m
Y el
centro de masa de la placa delgada será la suma de las masas de las tiras.
(8)
Ejemplo. La placa
triangular que se muestra en la figura tiene una densidad constante de 3g.cm2. encontrar
- El momento de la placa con respecto al eje x y el eje y
- La masa del plato.
- Coordenadas del centro de masa de la placa.
Podemos resolver este
problema utilizando dos métodos: el método de la franja vertical o el método de
la franja horizontal. Si usamos el método de la tira vertical.
Esta es una distribución de
masa sobre una región en el plano, así que para encontrar el momento sobre el
eje x y el eje y debemos usar las expresiones integrales.
Ahora el diferencial dm
es la masa de la tira que se puede aproximar como el producto de la densidad y
el área diferencial dA. si la densidad se define como una función
continua y el área de la tira se puede determinar por su largo por su ancho. En
el caso de nuestra tira elegida tenemos una densidad dada δ = 3 g.cm2
dA =
2x dx
por lo que nuestra
expresión para dm se convierte en
dm =
δdA = δ.2x dx = 6x dx
Para establecer la
integral. Necesitamos encontrar la coordenada (x̃, ỹ) en términos de x
e y, luego integramos ỹdm y x̃dm entre los límites de
integración determinados por la ubicación de la placa en el plano y la franja
elegida, ya que estamos usando una franja vertical definida por el ancho dx,
integramos en los límites del eje x 0 ≤ x ≤ 1. Una expresión para
las coordenadas.
La distancia promedio entre
el límite inferior y superior
ỹ = x
Es simplemente la distancia
x desde el eje de rotación. Así que ahora podemos encontrar el momento
con respecto a cada eje.
El momento sobre el eje
x.
El momento sobre el eje
y.
Ahora para la masa de la
placa usamos la expresión integral.
Como ya tenemos una
expresión para dm, podemos proceder a calcular.
Y las coordenadas del
centro de masa son.
Si nuestros cálculos son
correctos, cuando usemos el método horizontal deberíamos obtener los mismos
resultados.
usando tiras horizontales
Tenemos que hacer un
análisis similar, empezando por encontrar una expresión para dm. lo definimos
como antes dm = δ dA, pero esta vez dA está definido en la
dirección horizontal. La longitud es la diferencia entre el lado derecho y el
lado izquierdo.
Ancho = dy
Longitud = 1 – y /2 (esta es la expresión y = 2x)
reescrita en términos de y.
Las coordenadas x̃ y
ỹ serán diferentes porque la orientación es diferente. En este caso, x̃
estará determinado por la distancia promedio mientras tanto.
Los límites de integración
también cambiaron porque la orientación cambió 0 ≤ y ≤ 2.
La masa del plato.
El centro de masa.
La misma solución porque es
el centro de masa.
Encuentre el centro de masa
de una placa limitada arriba por la parábola y=4 - x2 y abajo por el eje x. La densidad de la placa es 2x2
Como en el problema
anterior, usamos nuestra integral. La distribución de masa es simétrica con
respecto al eje y, por lo que el centro de masa x̄ = 0. Podemos
usar el método de la franja vertical para encontrar ȳ, pero primero
debemos definir dm y x̃.
Como antes, definimos dm
= δdA. dA se puede definir por el ancho dx por el largo 4
– x2.
El momento sobre el eje
x
La coordenada del centro de masa es
Placas Delgadas Limitadas
Por Dos Curvas
Supongamos que una placa
cubre una región que se encuentra entre dos curvas g(x) y f(x)
donde f(x) ≥ g(x) y a ≤ x ≤ b. Creamos una franja vertical como
antes donde
Centro de masa de la tira: (x̃,
ỹ) = (x, ½ [f(x) – g(x)])
Altura o longitud: f(x)
– g(x)
Ancho: dx
Área: (f(x) – g(x))dx
Masa: dm = δ dA
El momento sobre el eje y:
Con estos podemos escribir
una fórmula para el centro de masa.
(9)
Encuentre el centro de masa
delimitado por las curvas en la siguiente figura.
Comencemos por calcular la
masa de la placa.
Entonces, el centro de masa con respecto a las x e y.
Centroides
En los casos que estudiamos
hasta ahora, el centro de masa se determinó en una distribución de densidad no
uniforme donde el centro geométrico y el centro de masa no son necesariamente
el mismo, hay otros casos donde la densidad de masa es constante y el centro de
masa es una característica de la geometría del objeto y no del material del que
está hecho. En estos casos, nos referimos al centro de masa como el centroide
de la forma. Para resolver este tipo de problema hacemos un análisis similar,
pero establecemos la densidad de masa δ = 1.
Encuentre el centro de masa
(centroide) de un alambre delgado de densidad constante con forma de
semicírculo de radio a.
La fórmula general para un
semicírculo es donde r es el radio.
La distribución de masa es simétrica con respecto al eje y, por lo que
el centro de masa del eje x es x̄ = 0. Para encontrar ȳ
debemos hacer lo mismo que hicimos antes, pero como estamos considerando un
alambre delgado, no no necesito el area sino el largo.
dm =
δds
con longitud ds = adθ
El punto ỹ se puede
encontrar usando trigonometría. ỹ = a sin(θ), y como es un semicírculo
tenemos 0 ≤ θ ≤ π.
Poniendo δ=1.
El centro de masa se
encuentra en el punto (0, 2a/π).
El δ se cancela en la ecuación, por lo que
podríamos haberlo igualado a 1 y obtenido el mismo valor.
Ahora
pueden seguirnos y contactarnos a través de Facebook, Twitter y correo
electrónico.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden
seguir nuestro otro blog si les interesa aprender sobre el interesante mundo de
la física.
- Facebook: https://www.facebook.com/JMDFisica
- Blogger: jmdfisica.blogspot.com