Geometría: Líneas y ángulos

    El contenido que estas a punto de leer está lleno de nuevas definiciones. Les recomiendo tomarse su tiempo a la hora de leer esta publicación y asegurarse que comprenden lo que aquí se describe. Si algo les resulta confuso y consideran que su definición es incorrecta pueden escribirlo en los comentarios.    

    En la previa publicación definimos una línea como una sucesión de puntos sin espacio entre ellos. Una línea no tiene ancho ni profundidad y es una dimensión en espacio. Una línea puede ser representada por una raya con flechas que indica que se extiende infinitamente en ambos lados. Podemos nombrarla usando dos puntos cualesquiera que pertenezcan a la línea y se vería así, esto indica que los puntos A y B son parte de la línea. Otro nombre común que se usa es el de la letra cursiva ℓ. Una línea carece de dirección, a menos que esta sea especificada en un plano, por lo tanto posee la siguiente propiedad.  y en el caso de que dirección es especificada.

    Si medimos la distancia entre dos puntos tendremos un segmento de línea. Esta no es infinita ya que tiene dos puntos al final que indican el límite de su tamaño. Un segmento de línea se nombra igual que una línea pero en vez de dos flechas solo usamos una barra para indicar que es finita.

    Existen líneas que también tienen un origen y se extienden al infinito en una sola dirección. Este tipo de líneas la llamamos rayo de línea. Cuando son nombradas la primera letra indica cual es el punto de origen y solo contiene una flecha. Esto también implica quepero  . A pesar de que este es el punto de origen del rayo es llamado punto final debido a errores de traducción. 

Representación gráfica de una línea, segmento de línea y rayo de línea.

    A la hora de dibujar líneas en un papel puede resultar un poco difícil crear una línea recta si esta es demasiado larga. No muchas personas pueden mantener el pulso de la mano para hacer una línea recta, yo incluido, pero existe una herramienta que nos ayuda a crear líneas perfectas y esta es la regla.

    Es un instrumento rectangular con forma de plancha delgada que incluye una escala longitudinal. Por lo general suelen ser de material rígido como la madera pero también existen flexibles como la cinta métrica que se usa en construcción. La longitud de la regla típica que encontramos en la escuela es de 15-30 centímetros, aunque existe reglas de 1 metro para usar en la pizarra. Está hecha a escala para medir y dibujar objetos en la escala de centímetros y milímetros, cada diez milímetros es un centímetro. Existen otros modelos que utilizan las pulgadas o fracciones de pulgadas como escala.

En una regla las pequeñas barras representan la distancia en milímetros mientras que los números indican centímetros.

    Las reglas se utilizan para trazar rectas, verificar la alineación o servir de guía, o para medir. Por lo general utilizamos el lado donde están los números y trazamos una línea a la distancia deseada partiendo por lo general desde cero, si empezamos desde cualquier otro punto entonces debemos recordar que ese punto es nuestro punto de partida y ajustar la medida acorde. Ejemplo una línea de 5 cm puede ir desde el punto 0 hasta el punto 5, o desde el punto 1 hasta el punto 6, o desde el punto 2 hasta el punto 7, etc.  

    Dos o más líneas crean propiedades interesantes dependiendo de la forma en que se presenten. Dadas dos líneas existen dos posibilidades:  ellas pueden que se intercepten en un punto o no. Aquellas líneas que se extienden al infinito y nunca se interceptan son consideradas líneas paralelas y se representan con el símbolo ‘//’. Dos líneas que se interceptan pueden crear líneas perpendiculares, expresada con el símbolo ⟂, formando ángulos de 90 grados entre sí o pueden crear líneas secantes cuyos ángulos difieren de los 90 grados. Existe una excepción y esta es las líneas coincidentes las cuales tienen todos sus puntos en común, es decir están una encima de la otra. Por lo general esto es ignorado pues se ve como solo una línea.

    Las líneas de la gráfica A son paralelas también se puede escribir como AB // CD mientras que las líneas de la gráfica B son perpendiculares y se expresan así DE ⟂ FG. La gráfica C presenta líneas secantes.

    Si dos líneas tienen un punto final en común entonces estas líneas forman lo que conocemos como un ángulo. Este punto final pasa a llamarse vértice. Y los rayos son conocidos como lados. Se representa con el símbolo ∠, no debe ser confundido con el símbolo < que significa “menor que”. 

    La figura representa el ángulo ∠ABC ó ∠CBA ó ∠B. La letra de en medio representa el vértice. Otra forma de describir un ángulo es usando la unión de dos rayos de líneas.  significa que el ángulo ABC es igual a la unión de los rayos BA y BC. Donde el punto en común y vértice es el punto B.

    Cuando dos líneas están interceptadas solo pueden moverse una dependiendo de la otra, esto hace que el número de ángulos posible sea limitado. La máxima amplitud de un ángulo es aquella donde uno de los lados se extiende lo más posible haciendo que este regrese a la posición de su origen y creando en el proceso un círculo. Por esta razón se considera que la amplitud de un ángulo es igual a un arco de circunferencia de un círculo. Su medida es basada en la proporción de la longitud del arco y el radio. Se mide en radianes pero la forma convencional es el uso del grado sexagesimal. 

    El instrumento utilizado para medir ángulos es el transportador y mide ángulos en grados. Por lo general el transportador que utilizamos en la escuela es de 180° pero existen transportadores de 360° e incluso transportadores en otra escala. 

Transportador con escala sexagesimal.

    Para crear un ángulo usando un transportador primero debemos crear una línea de referencia con respecto al ángulo de cero grados (1). El centro del transportador será donde vamos a localizar el vértice del ángulo (2), luego marcar el grado deseado ya sea 30°, 45°, 22° (3) y finalmente trazar una segunda línea desde la línea de referencia hasta el punto marcado (4).

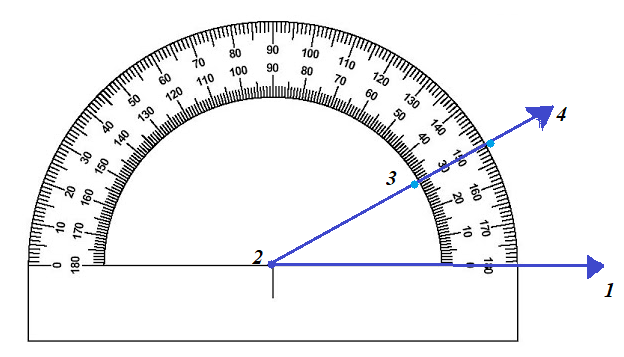
Descripción de como trazar un ángulo usando un transportador.

    De acuerdo con su amplitud los ángulos son clasificados como:

• Angulo nulo: es el ángulo formado por dos semirrectas coincidente y mide cero grados, es decir sin aberturas
• Angulo agudo: es todo Angulo cuya amplitud sea mayor que cero grados y menor que 90°. X es agudo si 0° < X < 90°.
• Angulo recto: es un ángulo cuya amplitud es 90°. Creando así dos líneas perpendiculares.
• Angulo obtuso: es todo ángulo cuya amplitud es mayor que 90° y menor que 180°.
• X es obtuso si 90° < X < 180°.
• Angulo llano: es un ángulo cuya amplitud es de 180°.
• Angulo oblicuo: es un ángulo que no es recto ni múltiplo de un ángulo recto. Los ángulos agudos y obtusos son ángulos oblicuos.
• Angulo completo: es un ángulo con una amplitud de 360°.

    Para convertir las unidades de los ángulos de grados a radianes y viceversa usamos la relación de que 180° es igual a π radianes y aplicamos la regla de tres. Ejemplo convertir 45° a radianes.

Si la suma de dos ángulos es igual a 90° entonces estos ángulos son complementarios.

Si la suma de dos ángulos es igual a 180°entonces estos ángulos son suplementarios.

    Por ahora esto será todo. Espero esto le sea de ayuda. Les dejare unos ejercicios sobre conversión de ángulos y ángulos complementarios y suplementarios. Si les gusto la publicación por favor compartir. En la próxima publicación estarán las respuestas a estos problemas.

Convertir los siguientes ángulos.

135° a radianes

3π/4 a grados

60° a radianes

2π/5 a grados

π/6 a grados

275° a radianes

¿Cuál es el ángulo complementario de 35°?

¿Cuál es el ángulo suplementario de 76°?

Dos ángulos son complementarios y sus ángulos miden 2x+5 y 3x-20. ¿Cuáles son los ángulos?

 

Geometría: Introducción

    La palabra geometría es una combinación de la palabra griega “geo-” que significa tierra y “-métrica” que significa medida. Es una de las ramas de las matemáticas más elegantes ya que trata de formas visuales que conocemos de la vida cotidiana, pero utiliza pruebas precisas.

    Aprender geometría no requiere habilidades previas como aritmética básica. Por lo tanto, la geometría es adecuada como introducción a las matemáticas para la escuela primaria y su aprendizaje es completamente lineal lo que permite que cualquier persona la aprenda en cualquier momento.

    La geometría que se estudia en el plano (aquella por la cual conocemos las diferentes figuras geómetras) se le conoce como geometría euclidiana, en honor al matemático griego Euclides quien escribió el libro más famoso de matemática y el segundo más leído en la historia.  

    Considerado el padre de la geometría debido a su gran aporte al campo con su libro “elementos” que está compuesto de 13 volúmenes, Euclides presenta la información que no se asume ser verdadera, se muestra. Empezamos desde un numero de axiomas que establecen la fundación de la geometría. Todo el material es derivado y probado consistente con los axiomas. Es esta forma única de presentar la información que hizo de su libro tan famoso. La gente no era considerada como educada si ellos no tenían conocimiento del Libro “Elementos” de Euclides por más de 2000 años después de su publicación.

    En su libro es presento cinco postulados que presentaban los conocimientos geométricos de la Grecia antigua. Los postulados de son:

1. ,Dos puntos distintos cualesquiera determinan un segmento de recta.

   

   
   

2. Un segmento de recta se puede extender indefinidamente en una línea recta.

   

   
   

3. Se puede trazar una circunferencia dados un centro y un radio cualquiera.

   

4. Todos los ángulos rectos son iguales entre sí.

   

   
   
   

5. Si una línea recta corta a otras dos, de tal manera que la suma de los dos ángulos interiores del mismo lado sea menor que dos rectos, las otras dos rectas se cortan, al prolongarlas, por el lado en el que están los ángulos menores que dos rectos.

    Este ultimo postulado es menos obvio que los demás, pero cuando se intento comprobar termino creando dos nuevas geometrías: la geometría hiperbólica también conocida como geometría de Lobachevsky y la geometría elíptica también conocida como geometría de Riemann. El propósito de esto es entender los fundamentos para explorar mas complicadas formas en el futuro.

“Las leyes de la naturaleza no son más que los pensamientos matemáticos de Dios” - Euclides.

    Así como Euclides nosotros vamos a basar nuestro estudio de la geometría empezando por crear el conjunto de axiomas que servirán de base para todo el trabajo que haremos en el futuro y a medida que nuevas cosas empiecen aparecer iremos describiendo como estos axiomas juegan un papel importante.

    Empezaremos por definir conceptos importantes para la fundación de la geometría. Puntos, líneas y tipos de líneas, ángulos y tipos de ángulos, rotaciones, reflexiones, traslaciones y dilataciones así también como las herramientas usadas en geometría. También debemos tener presente el significado de la nomenclatura. Algunos de los símbolos que vamos a encontrar serán.

    Las letras elegidas son irrelevantes, lo importante es reconocer que cuando presentemos información de esta forma sepan a qué nos referimos. Empecemos con definiciones importantes.

    Los objetos mas simples en la geometría son el punto, la línea y el plano. Esta simplicidad hace que sea difícil dar una definición exacta de lo que son, pero podemos construir una basada en sus propiedades.

    Un punto se utiliza para marcar una posición en el espacio y no contiene estructura interna, no tiene tamaño. Cuando dibujamos un punto es obvio que este tiene dimensiones (tal vez al nivel de micrómetros o nanómetro) pero en realidad es solo una representación de un objeto que no tiene ninguna estructura solo representa una marca en una posición. Representamos un punto con una letra mayúscula

    Una sucesión de puntos sin espacio entre ellos nos ayuda a formar lo que es una línea. Una línea no tiene anchura y se extiende hasta el infinito por ambos lados. Por lo general se representa con dos flechas en los extremos que indican que se extiende. De un punto se pueden crear infinitas líneas en todas las direcciones. Entre dos puntos podemos crear lo que llamamos un segmento de una línea. Podemos nombrar un segmento de línea usando los nombres de los puntos con un marcador arriba que indica si es una línea o un segmento. Usamos la doble flecha (↔) para indicar que es una línea usamos una barra (-) para indicar que es un segmento de línea.

    Un plano es una superficie plana, que se extiende infinitamente. Tiene largo y ancho pero no profundidad, un espacio bidimensional. La parte superior de una mesa, un piso o una pared es parte de un plano. Podemos nombrar un plano usando cualquiera de los tres puntos que se encuentran en el plano. La idea de un plano que se extiende infinitamente es prácticamente imposible pero secciones de un plano como una hoja de papel la usamos como referencia en el día a día.

    La idea del infinito es algo más allá de lo que podemos construir sin embargo su uso es bastante importante. En geometría podemos usar escala para determinar propiedades ya que las propiedades deben mantenerse tanto en el finito como en lo infinito.

    Con esto hacemos nuestra introducción a la geometría. En la próxima publicación estaremos hablando sobre líneas. No olviden compartir y dejar sus comentarios