Multiplicación de Binomios
Los
binomios tienen algunas características con respecto a la multiplicación que
hace los cálculos más simples.
Si
un binomio es multiplicado por sí mismo es igual que ser elevado al cuadrado.
(2x2 +3y)
* (2x2 +3y) = (2x2 +3y)2
La multiplicación de un binomio por su conjugado es igual a
la diferencia del cuadrado de los
términos.
(a + b) *
(a - b) = a2 – b2
Cuando tenemos un binomio
elevado al cuadrado podemos aplicar una técnica llamada binomio de newton. “el
primer monomio es elevado al cuadrado, más dos multiplicado por el primer y
segundo monomio, más el segundo monomio al cuadrado.”
(2x2 +3y)2
= (2x2)2 + 2(2x)(3y) + (3y)2
4x4 + 12xy + 9y2
Demostración
Recordatorio:
en la multiplicación los exponentes de la misma letra se suman y los
coeficientes se multiplican
·
División de polinomios
A diferencia de la multiplicación, en la división los
exponentes se restan y los coeficientes se dividen. Como toda división contamos con un dividendo
(el polinomio que se va a dividir) y un divisor (el polinomio que divide).
Un ejemplo simple para mostrar los pasos:
Resultado: X2
En este ejemplo vemos los pasos a seguir para realizar una
simple división pero como podemos trabajar un problema como el siguiente:
x5 + 2x3 − x – 8 ÷ x2 − 2x + 1
Para trabajar con un problema así debemos seguir los
siguientes pasos.
1.
Los polinomios deben ser organizado en orden
descendente (de mayor a menor) según sus exponentes, si hay algún exponente
faltante se expresa con un espacio en blanco o con el numero 0 (cero) ya que
cualquier numero multiplicado por cero es igual a cero.
2.
Se divide el primer monomio del dividendo entre
el primer monomio del divisor.
3.
El resultado de esta división se multiplica por
cada uno de los términos del divisor.
4.
El resultado de esta división es restado del
dividendo.
5.
El proceso se repetirá hasta que el grado del
dividendo sea menor que el del divisor o el divisor sea igual a cero.
Ejemplo:
(11x2
+ 6 - 5x3 + x4 - 12x) ÷
(-3x + x2 + 3)
1er paso: organizar en forma descendente.
2do
paso: dividir el primer monomio del dividendo entre el primer monomio del
divisor.
3er
paso: multiplicar por cada término del divisor.
4to
paso: restar los términos semejantes.
5to
paso: repetir todo el proceso hasta que el grado del dividendo sea menor
que el del divisor o el divisor sea igual a cero.
Otro ejemplo
Las reglas
para la división de fracciones también se aplican para los polinomios.
A veces el
divisor es simplemente un monomio. Esto facilita la división ya que al tener un
solo término podemos dividir directamente.
con esto concluimos las operaciones básica de los polinomios. para el próximo post empezaremos explicando las variables y ecuaciones y luego regresaremos con nuevas operaciones de polinomios.








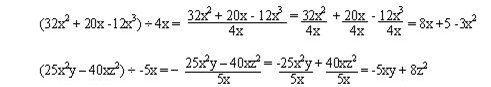
No hay comentarios.:
Publicar un comentario