El método de rebanar a veces puede ser complicado de implementar dependiendo de la forma del sólido, así que busquemos otra forma de rebanar para estos casos.
En
el caso presentado arriba, tenemos la gráfica de la función y = -3x2 + 7x
en la parte A. como hemos visto antes, giramos nuestra función paralelamente al
eje que está definido y podemos aplicar el método del disco para resolver el
volumen (parte B), pero si giramos la función perpendicular al eje en el que se
define la revolución (parte C), y tratamos de usar el método de la arandela
para eso, debemos reescribir la ecuación en términos de y, lo que creará
una muy complicada fórmula, ya que también seguirá siendo dependiente de x
y aún no sabemos cómo evaluar esto. Esto sucede porque el método de la arandela
y el disco se integran a lo largo del eje paralelo al eje de rotación. Debemos
crear un método que nos permita integrar perpendicularmente al eje de
revolución.
En el ejemplo dado, en lugar de rotar una tira horizontal de espesor ∆y (paralela al eje de rotación), rotamos una tira vertical de espesor ∆x (perpendicular al eje de rotación) produciendo una capa cilíndrica de altura yk sobre un punto xk. Seguimos haciendo esto hasta que todos los cilindros sigan el contorno de la parábola.
Cada
rebanada se asienta sobre un subintervalo de la longitud del eje x. Su
radio es aproximadamente (1 + xk) y su altura está
determinada por -3x2 + 7x. Si desenrollamos el cilindro y lo
aplanamos se convierte aproximadamente en una losa rectangular de espesor ∆xk,
la longitud viene dada por la circunferencia exterior 2πradio = 2π(1+xk). El volumen de
esta losa rectangular se aproxima como si fuera un sólido rectangular.
Sumando
todos los cilindros individuales obtenemos una suma de Riemann, y seguimos los
mismos pasos que en publicaciones anteriores.
Esto
es lo esencial del método de caparazón. Ahora generalicemos el procedimiento
para obtener una fórmula general.
En la figura de arriba, tenemos una región limitada por la función y = f(x) y debajo por el eje x y las líneas x=a y x=b para el límite izquierdo y derecho respectivamente. Anteriormente, las regiones definidas en función de x se giraban alrededor del eje x o paralelas a él, pero esta vez las giraremos alrededor del eje y.
Para calcular su volumen como lo hemos hecho muchas veces antes, dividimos el intervalo y construimos rectángulos de altura f(xk) y ancho ∆x. cuando se gira un rectángulo, obtenemos una cubierta cilíndrica en lugar de un disco o una arandela.
El
volumen del cilindro es el área de la sección transversal multiplicada por la
altura del cilindro. Las secciones transversales son regiones en forma de
anillo esencialmente con un radio exterior xi y un radio
interior xi-1. Por lo tanto, el área de la sección transversal
es πxi2
– πxi-12 y el volumen.
Note que (xk
- xk-1) = ∆x
Sumando
todas las conchas, aproximamos el volumen de la región R.
En resumen, sea F(x) una función continua y no negativa. Defina R como la región limitada arriba por la gráfica de F(x), abajo por el eje x, a la izquierda por la línea x=a y a la derecha por la línea x=b. Entonces, el volumen del sólido de revolución formado al hacer girar R alrededor del eje y está dado por
Ejemplos.
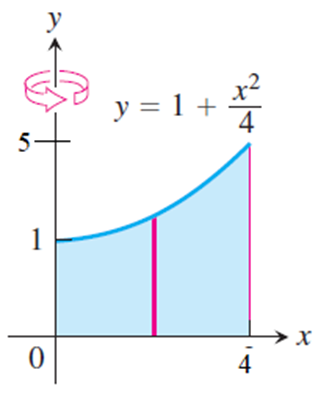
- Use el método de la cáscara para encontrar los sólidos de volumen generados al girar la región sombreada alrededor del eje indicado.
Si
giramos alrededor del eje y como se indica, obtenemos la siguiente forma.
La
región sombreada se define a partir de 0 ≤ x ≤ 4, por lo que podemos
poner nuestra función directamente en nuestra fórmula derivada y calcular el
volumen.
Las
funciones están dadas en términos de y por lo que integramos con
respecto a y. tenemos que nuestra función se define a partir de 0 ≤ y
≤ √2
Si giramos alrededor del eje y como se
indica, obtenemos la siguiente forma.
Encuentre el volumen del sólido de revolución generado al hacer girar la región R limitada arriba por la gráfica de la función f(x) = √x y abajo por la gráfica de la función g(x) = 1/x en el intervalo [1, 4] alrededor del eje y.
Sin embargo, la altura de una
capa viene dada por la diferencia f(x)−g(x), por lo que en este caso
necesitamos ajustar el término f(x) del integrando. Entonces el volumen
del sólido está dado por.
Podemos reescribir esta
expresión de la siguiente manera,
En resumen, obtenemos los tres
métodos para la sección transversal y sus características en la siguiente
tabla.
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden seguir nuestro otro blog si les
interesa aprender sobre el interesante mundo de la física.
- Facebook: https://www.facebook.com/JMDFisica
- Blogger: jmdfisica.blogspot.com











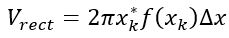















No hay comentarios.:
Publicar un comentario