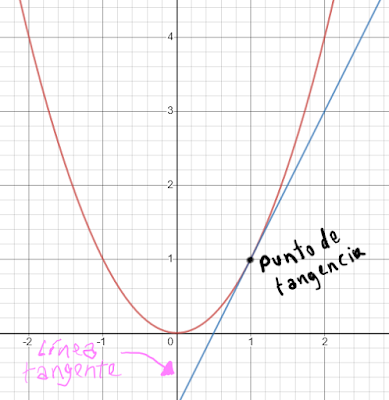
Para hablar sobre las derivadas debemos primero tener en claro los conceptos de línea tangente y línea secante. La línea tangente es una recta que toca a la curva de una gráfica sólo en un punto llamado punto de tangencia.
Una línea secante es una recta que corta una curva en dos puntos. Conforme estos puntos se acercan y la distancia se reduce a cero, la recta adquiere el nombre de recta tangente.
Para encontrar la tangente a una curva y = f (x) en un punto P (x0, f (x0)) calculamos la pendiente de la secante a través del punto P y un punto cercano Q (x0 + h, f (x0 + h)) donde h es una cantidad arbitraria, entonces tomamos el límite de la pendiente cuando h → 0.Si el límite existe, lo llamamos la pendiente de la curva que podemos definir en el punto P (x0, f (x0 )) como m.
La expresión f se llama cociente de diferencias de f en x0 con incrementos h y el límite de esta expresión es lo que llamamos la derivada de una función f en el punto x0 y denotamos como f '(x0) esto muestra que la derivada es la pendiente de una recta secante en cualquier punto x0; f '(x0) = m.
Ejemplo encuentra la derivada de f(x) = x2 cuando x = 5
f '(5) = 2(5) = 10
Otro ejemplo. Calcula f '(3) donde f(x) = 4x2 - 7x
1ero vamos a calcular f' (x)
Evaluando cuando x = 3
f '(3) = 8(3) - 7 = 24 - 7 = 17
Teorema 1
El proceso de calcular una derivada se llama diferenciación. Usamos la notación 
para implicar que la diferenciación se realiza en la función f (x). Otra forma de expresarlo es f '(x) como se muestra en los ejemplos. Otra notación es 
para indicar que la derivada se performa en la variable x y 
para indicar que la derivada está siendo evaluada en el punto x = a.
